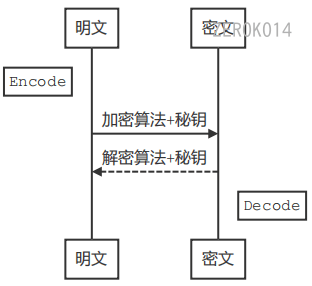
加密与解密

ZEROKO142023-11-242024-12-21

加解密相关知识及其背后原理阐述

加解密相关

涉及到网络数据传输的且对传输的数据有安全性需求的,就需要传输数据之前对数据进行加密操作,常用的网络通信方式有

socket通信 —- 如 socket API编程
http协议通信 —- 如B/S模式

为保证网络通信时数据的安全,就需要对数据进行加密

常用的加密的方式

对称加密

加密和解密使用的是同一个秘钥

秘钥分发困难
加密效率高
安全级别低(相对与非对称加密)

AEAD解密方式

非对称加密

非对称加密可靠的前提在于: 对方真的是对方,非对称加密害怕被冒充

加密和解密所使用的秘钥不同,是一个秘钥对,包含:

公钥 — 可以公开的秘钥
私钥 — 不能公开的秘钥

传输的数据对谁更重要,谁就拿私钥

私钥加密,公钥解密的场景:可以用于确定该信息来自私钥拥有者
公钥加密,私钥解密的场景:可以用于向私钥拥有者传递数据防止被其他人解密

加密的过程:使用公钥加密,必须使用私钥解密;使用私钥加密,必须使用公钥解密

秘钥分发简单
加密效率低
安全级别高

加密需要实现:

秘钥生成,秘钥校验
秘钥生成模块应该与实际使用该模块的项目关联程度要低,耦合度要低,一个模块的修改不要影响其他模块

最简单的非对称加密方式举例

想一个数字,将他乘以2359得到的数取后五位

将取到的后五位数乘以12039,得到的五位数就是最开始的数字

原理是2359*12039为28400001,因此它天然可以保留后五位数,也知道刚开始想的数字最多为5位数

这种加密,知道2359后,可以推出12039,破解加密算法

常用安全算法

对称加密

DES/3DES

DES-已经被破解

要求秘钥长度8字节
在对数据进行加密之前先对数据按每组8个字节进行分组,然后分段进行加密,最后再将每一段加密的数据进行组合

3DES-效率低

秘钥长度24字节,内部会将秘钥分成3份
同样,需要加密的数据先按每组8个字节进行分组,然后分别使用三份秘钥进行加密—>解密—>加密;
若三份秘钥都相同,其实就是DES加密方式

AES

使用最广泛的对称加密算法,详解

秘钥要求:

16字节,24字节,32字节
秘钥长度越大,加密效率越低,但安全性越高

其他对称加密算法

TDEA
Blowfish
RC2/RC4/RC5
IDEA
SKIPJACK

非对称加密

RSA(数字签名和密钥交换)
ECC(椭圆曲线加密算法)
Diffie-Hellman(DH,密钥交换)
El Gamal(数字签名)
DSA (数字签名)

DH算法原理

迪菲-赫尔曼 Diffie–Hellman 密钥交换算法
DH 算法的关键在于离散对数问题的难解性，即在已知 A、B 和 $A^x \bmod B$ 的情况下，计算 x 的困难性。这使得攻击者无法通过截获网络传输的公钥来推导出私钥，从而保证了密钥交换的安全性。
5 和 23 就是上面的 A 和 B 是公开的数字可以任意更换:
需要了解一个公式: $(5^x \bmod 23 )^y \bmod 23= (5^x \bmod 23 )^y \bmod 23=5^{xy} \bmod 23$
$$
(A^x \bmod B )^y \bmod B= (A^x \bmod B )^y \bmod B=A^{xy} \bmod B
$$
这个公式展示了 Diffie-Hellman 算法的交换性质，即指数运算和模运算的顺序不会影响最终的共享密钥。

RSA算法原理

用于生成非对称加密的公私钥

数学原理参考1

数学原理参考阮一峰

RSA算法数学原理视频|720x360

明文,密文转化过程如图:

161675332249_.pic

公钥,私钥生成规则:

171675332251_.pic

RSA算法流程

找到两个指数p,q，计算其乘积n
计算t = （p-1）*（q-1） (欧拉函数)
选择一个整数E使得gcd(E,t)=1

gcd是最大公约数greatest common divisor
找到一个整数D使得E*D/t的余数为1,即Ex-yf-1=0(x,y为整数)
公钥为n,E 私钥为n,D

加密:
$$
密文 = 明文^{E} \bmod n
$$

$$
明文 = 密文^{D} \bmod n
$$

Hash算法

Hash算法 –> 单向散列函数 —- Hash算法不是用于加密的,只能单向转换

将任意长度的数据生成一个固定长度的字符串
MD4/MD5
- 散列值长度16字节
SHA-1
- 散列值长度20字节
SHA-2
- SHA224/SHA256/SHA384/SHA512
- sha224
  - 散列值长度:224/8=28字节
SHA3-224/SHA3-256/SHA3-384/SHA3-512
HMAC

注意:Hash算法由于不能逆,所以不能得到原始数据,不能用于加密,多用于数据校验

消息认证码

消息认证码(message authentication code)是一种确认完整性并进行认证的技术,取三个单词的首字母,简称为MAC.

消息认证码的输入包括任意长度的消息和一个发送者与接受者之间共享的密钥,它可以输出固定长度的数据,这个数据称为MAC值.

根据任意长度的消息输出固定长度的数据,这一点和单向散列函数很类似.但是单向散列函数中计算散列值时不需要密钥,而消息认证码中则需要使用发送者与接受这之间共享的密钥.

上面的hmac就属于消息认证码

数字签名

openssl配置

OpenSSL 是一个安全套接字层密码库(由C语言实现的)，囊括主要的密码算法、常用的密钥和证书封装管理功能及SSL协议，并提供丰富的应用程序供测试或其它目的使用。

SSL是Secure Sockets Layer（安全套接层协议）的缩写，可以在Internet上提供秘密性传输。Netscape公司在推出第一个Web浏览器的同时，提出了SSL协议标准。其目标是保证两个应用间通信的保密性和可靠性,可在服务器端和用户端同时实现支持。已经成为Internet上保密通讯的工业标准.https协议就用到了SSL,HTTPS协议是由SSL+HTTP协议构建的可进行加密传输,身份认证的网络协议,比http协议安全

OpenSSL既可以在windows平台下使用,也可以在linux平台下使用,是开源跨平台的一套加密库

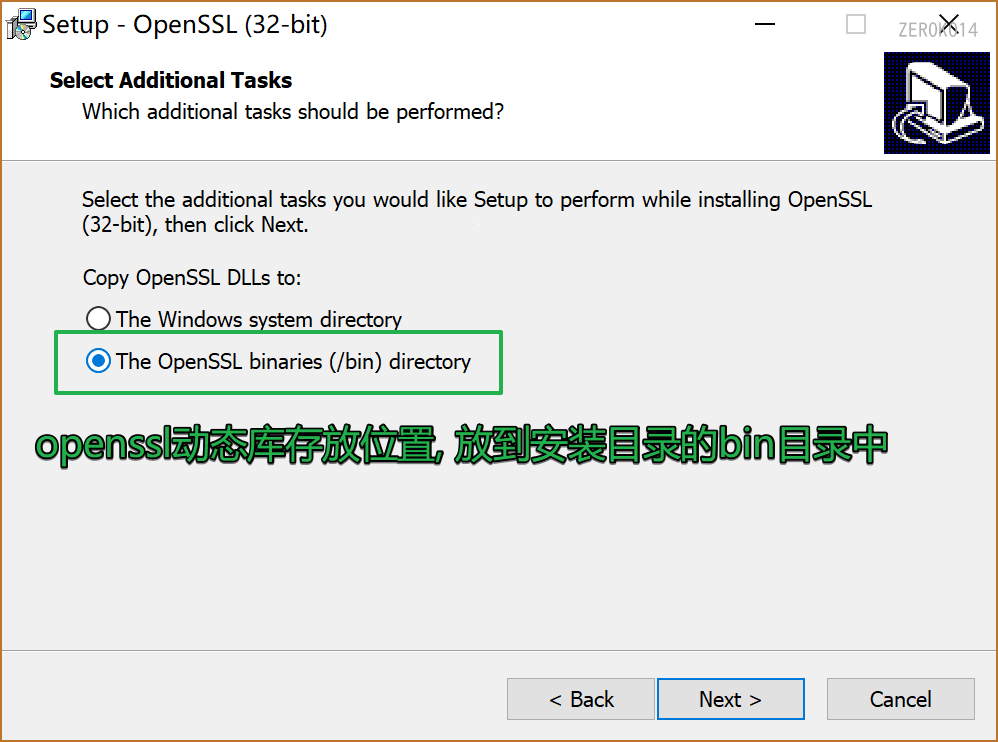
win下安装

OpenSSL win版安装路径

win下使用openssl

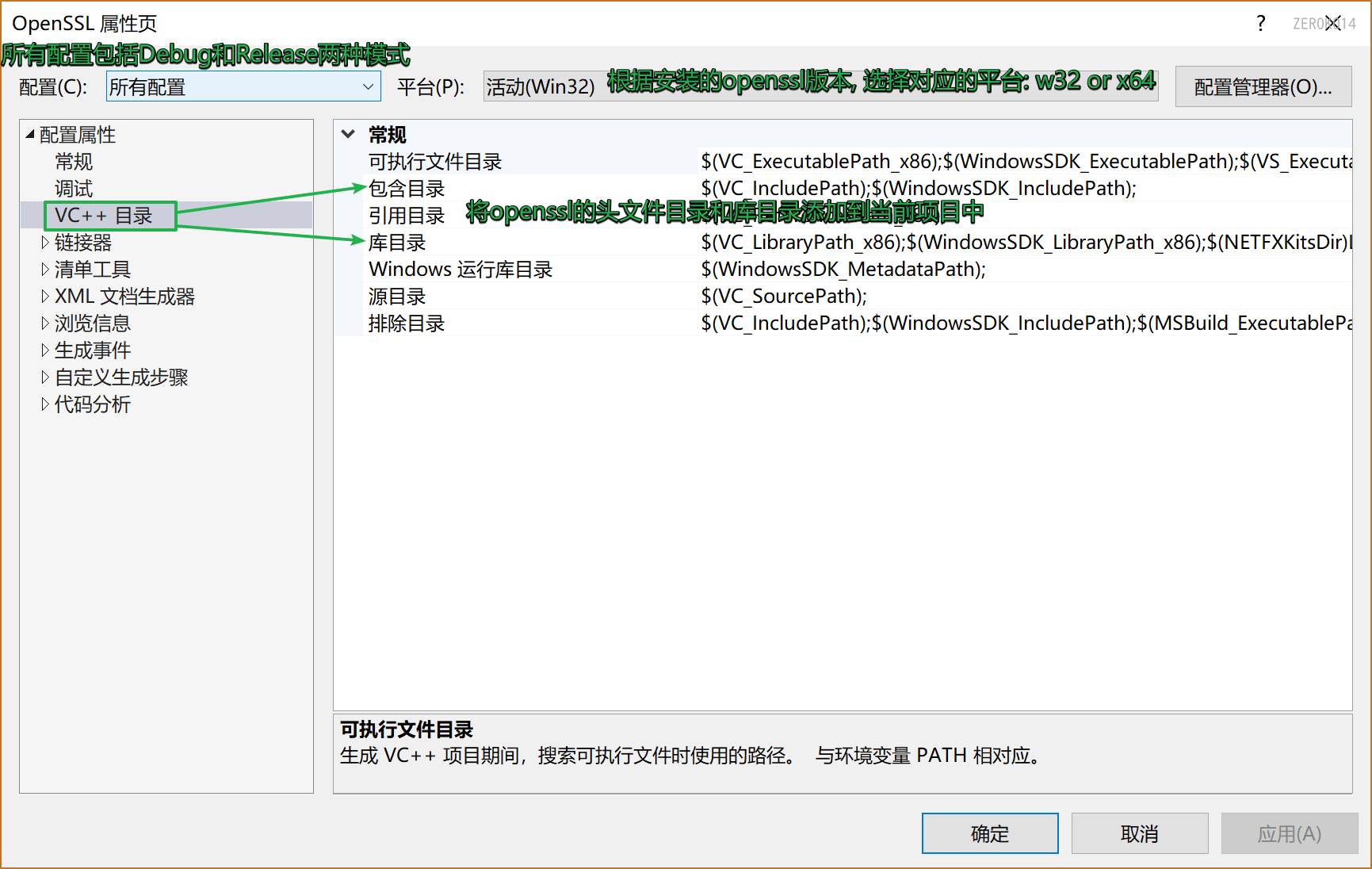
设置项目属性,将openssl的头文件目录和库目录添加到当前项目中

包含目录设置为openssl安装目录下的include目录
库目录设置为openssl安装目录下的lib目录

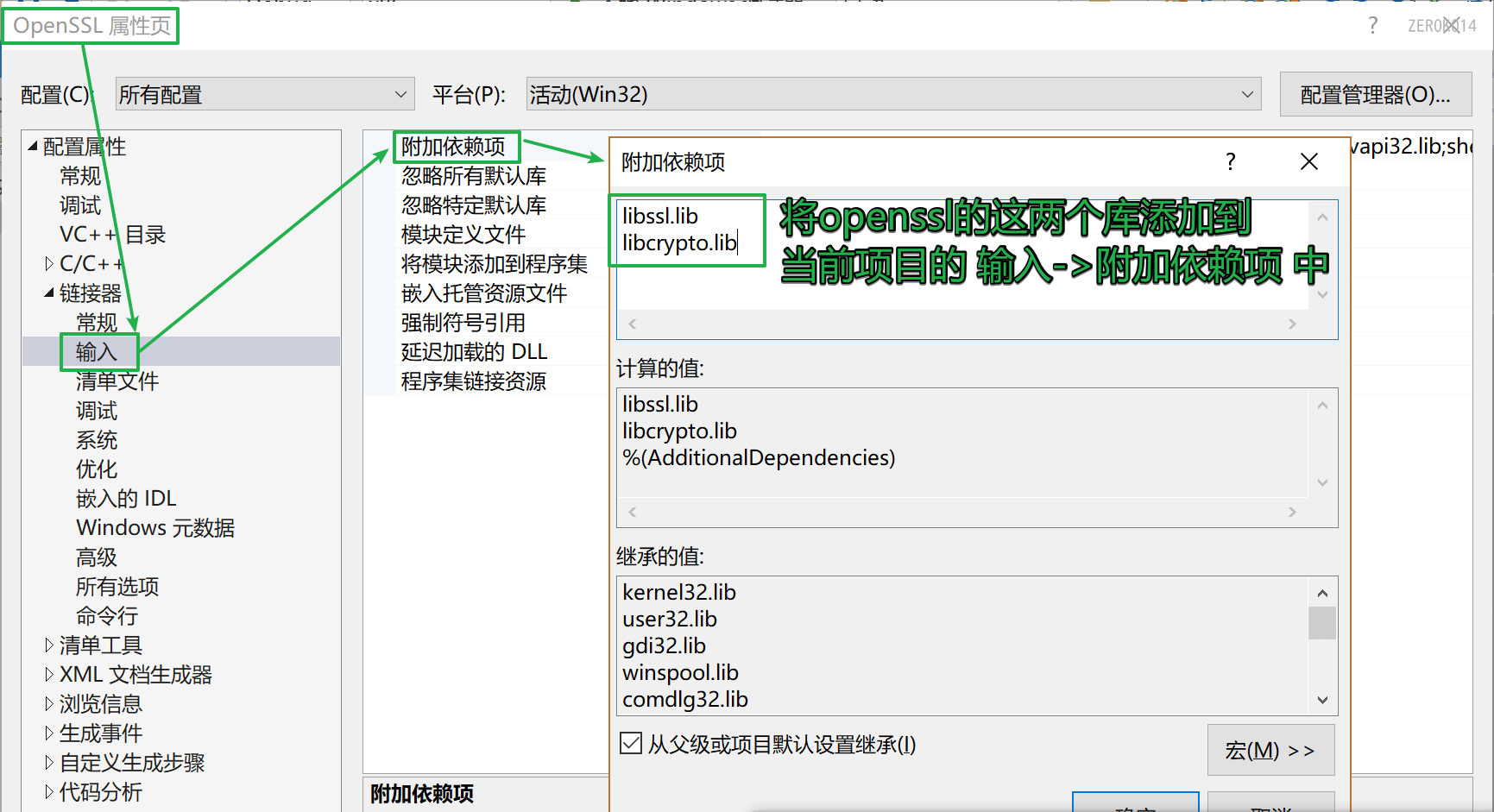
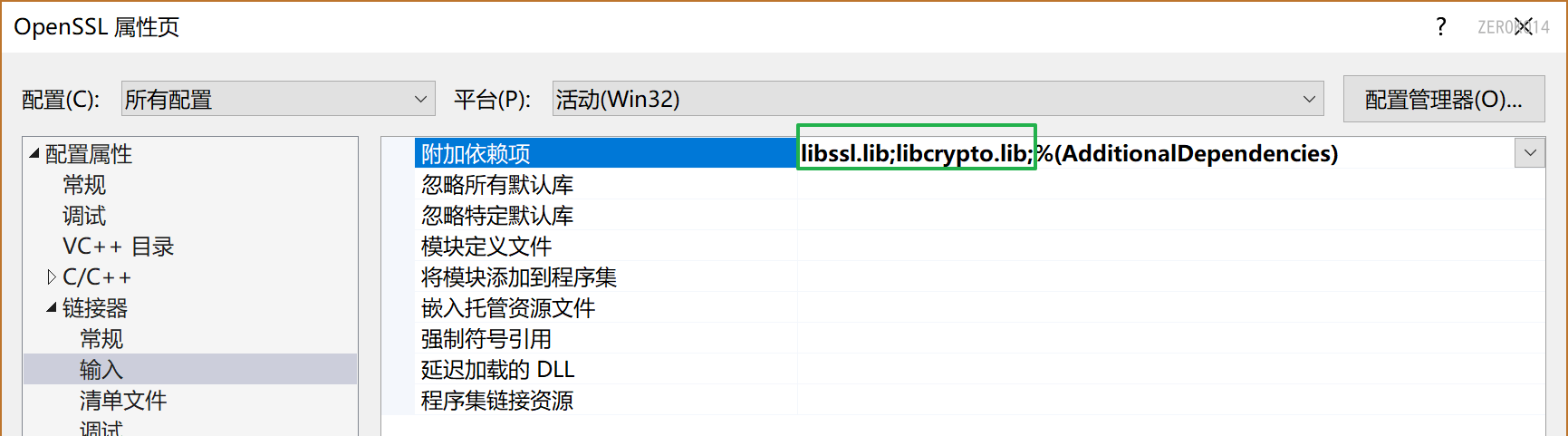
VS中的附加依赖项设置:

项目属性 -> 链接器 -> 输入 -> 附加依赖项

libssl.lib
libcrypto.lib

将openssl安装目录/bin目录下的两个动态库拷贝到工作目录下:

libcrypto-1_1-x64.dll
libssl-1_1-x64.dll

测试代码:

#define _CRT_SECURE_NO_WARNINGS
#include <openssl/md5.h>    // md5 头文件
#include <stdio.h>
#include <string.h>
#include <stdlib.h>

void getMD5(const char* str, char* result)
{
  MD5_CTX ctx;
  // 初始化
  MD5_Init(&ctx);
  // 添加数据
  MD5_Update(&ctx, str, strlen(str));
  // 计算结果
  unsigned char md[16] = { 0 };
  MD5_Final(md, &ctx);
  for (int i = 0; i < 16; ++i)
  {
    sprintf(&result[i * 2], "%02x", md[i]);
  }
}

int main()
{
  char result[33] = { 0 };
  getMD5("hello, md5", result);
  printf("md5 value: %s\n", result);
  system("pause");
  return 0;
}

输出:

1 2	输出结果: md5 value: 33b3bc8e05b4fcc16bd531dd9adac166

Linux下安装

OpenSSL linux版下载

git clone https://github.com/openssl/openssl.git

进入根目录,安装:

./config
make
make test    (可选)
make install   (使用管理员权限执行该命令)

参考[[linux基础以及系统编程#linux源码安装]]中的安装流程:

以下文件, 里边有安装步骤

readme

readme.md

INSTALL

找可执行文件 configure

执行这个可执行文件

检测安装环境

生成 makefile

执行make命令

编译源代码

生成了动态库

静态库

可执行程序

安装 make install (需要管理员权限)

将第三步生成的动态库/动态库/可执行程序拷贝到对应的系统目录

验证是否安装成功

openssl version -a

Linux下使用openssl

使用的代码与此处代码一样

通过gcc编译源文件

gcc md5_test.c -o md5 -lssl -lcrypto
执行该命令, 需要加载openssl的两个动态库    
- libssl.so    
- libcrypto.so

查看生成的可执行程序 md5 运行时需要加载的动态库:

ldd md5

如果找不到,可以使用定位libcrypto.so locate libcrypto.so 或者 find / -name "libcrypto.so"等语句找到动态库所在目录

将找到的动态库绝对路径添加到 /etc/ls.so.conf 文件夹中,并使用管理员权限执行命令 ldconfig

sudo vim /etc/ld.so.conf
将 找到的动态库绝对路径 添加到文件末尾, 保存退出配置文件
更新配置:
sudo ldconfig

BIO

BIO（BIO - I/O abstraction）是OpenSSL库中提供的一个I/O抽象层。它提供了一种统一的接口，用于对不同类型的数据源（如文件、内存、网络连接等）进行读写操作。

BIO提供了一种灵活的方式来处理数据的输入和输出，无论是从文件读取数据，还是将数据写入文件，甚至是通过网络发送数据，都可以通过BIO来实现。它可以用于加密、解密、签名、验证等各种加密操作。

BIO可以与各种数据源进行交互，包括文件（FILE*）、内存缓冲区（buffer）、套接字（socket）等。它提供了一组函数，如BIO_new()用于创建BIO对象，BIO_read()和BIO_write()用于读写数据，BIO_free()用于释放BIO对象等。

BIO的优点是可以将不同类型的数据源抽象为统一的接口，使得代码更加灵活和可移植。在加密和解密操作中，BIO常用于将密钥、证书、加密数据等读取到内存中，或者将加密结果写入文件或发送到网络中。

需要注意的是，BIO在使用时需要进行适当的错误处理和内存管理，以确保安全和可靠的数据传输。

BIO相关api

BIO *BIO_new(BIO_METHOD *method) 创建一个内存BIO对象
BIO *BIO_new_file(const char *filename, const char *mode)：创建一个新的文件BIO对象，并打开指定的文件。
BIO_new_fd(int fd, int close_flag)：创建一个新的文件描述符BIO对象，并关联指定的文件描述符。
BIO_new_socket(int sock, int close_flag)：创建一个新的套接字BIO对象，并关联指定的套接字。
int BIO_write(BIO *bio, const void *data, int dlen)：将数据写入 BIO 对象。
int BIO_read(BIO *bio, void *data, int dlen)：从 BIO 对象中读取数据。
int BIO_puts(BIO *bio, const char *str)：将字符串写入 BIO 对象。
int BIO_gets(BIO *bio, char *buf, int size)：从 BIO 对象中读取字符串。
int BIO_flush(BIO *bio)：刷新 BIO 对象。
int BIO_set_close(BIO *bio, long c)：设置 BIO 对象是否关闭。
long BIO_ctrl(BIO *bio, int cmd, long larg, void *parg)：控制 BIO 对象的行为。
void BIO_free_all(BIO *bio)：释放 BIO 对象的内存空间。

RSA算法api

OpenSSL库中提供了一系列RSA相关的函数，以下是其中一些常用的函数及其作用

下面需要的两个头文件为 <openssl/rsa.h> 和 <openssl/pem.h>

RSA_new()：创建一个空的RSA对象。
RSA_generate_key_ex()：生成RSA密钥对。
RSA_size()：获取RSA密钥的长度。
RSA_public_encrypt()：使用RSA公钥加密数据。
RSA_private_decrypt()：使用RSA私钥解密数据。
RSA_private_encrypt()：使用RSA私钥加密数据。
RSA_public_decrypt()：使用RSA公钥解密数据。
PEM_write_RSA_PUBKEY()：将RSA公钥以PEM格式写入文件。
PEM_write_RSAPrivateKey()：将RSA私钥以PEM格式写入文件。
PEM_read_RSA_PUBKEY()：从PEM格式的文件中读取RSA公钥。
PEM_read_RSAPrivateKey()：从PEM格式的文件中读取RSA私钥。
RSA_free()：释放RSA对象占用的内存。

详细含义参阅下方:(一一对应)

RSA* RSA_new()：创建一个空的RSA对象。
- 返回值：指向新创建的RSA对象的指针
int RSA_generate_key_ex(RSA* rsa,int bits,BIGNUM* e,BN_GENCB* c)：生成RSA密钥对。
- rsa：指向RSA对象的指针
- bits：生成密钥对的位数
- e：公钥指数
- cb：进度回调函数指针（可选）
- 返回值：成功返回1，失败返回0
int RSA_size(const RSA* rsa)：获取RSA密钥的长度。
- 参数：rsa：指向RSA对象的指针
- 返回值：RSA密钥的长度（以字节为单位）
int RSA_public_encrypt(int flen, const unsigned char* from, unsigned char* to, RSA* rsa, int padding)：使用RSA公钥加密数据。
- flen：要加密的数据长度（以字节为单位）
- from：指向要加密的数据的指针
- to：指向存储加密结果的缓冲区的指针
- rsa：指向RSA对象的指针
- padding：填充方式
- 返回值：加密后的数据长度
int RSA_private_decrypt(int flen, const unsigned char* from, unsigned char* to, RSA* rsa, int padding)：使用RSA私钥解密数据。
- flen：要解密的数据长度（以字节为单位）
- from：指向要解密的数据的指针
- to：指向存储解密结果的缓冲区的指针
- rsa：指向RSA对象的指针
- padding：填充方式
- 返回值：解密后的数据长度
int RSA_private_encrypt(int flen, const unsigned char* from, unsigned char* to, RSA* rsa, int padding)：使用RSA私钥加密数据。
- flen：要加密的数据长度（以字节为单位）
- from：指向要加密的数据的指针
- to：指向存储加密结果的缓冲区的指针
- rsa：指向RSA对象的指针
- padding：填充方式
- 返回值：加密后的数据长度
int RSA_public_decrypt(int flen, const unsigned char* from, unsigned char* to, RSA* rsa, int padding)：使用RSA公钥解密数据。
- flen：要解密的数据长度（以字节为单位）
- from：指向要解密的数据的指针
- to：指向存储解密结果的缓冲区的指针
- rsa：指向RSA对象的指针
- padding：填充方式
- 返回值：解密后的数据长度
int PEM_write_RSA_PUBKEY(FILE* fp, RSA* rsa)：将RSA公钥以PEM格式写入文件。
- fp：文件指针，指向要写入的文件
- rsa：指向RSA对象的指针
- 返回值：成功返回1，失败返回0
int PEM_write_RSAPrivateKey(FILE* fp, RSA* rsa, const EVP_CIPHER* enc, unsigned char* kstr, int klen, pem_password_cb* cb)：将RSA私钥以PEM格式写入文件。
- fp：文件指针，指向要写入的文件
- rsa：指向RSA对象的指针
- enc：加密算法（可选）
- kstr：密码字符串（可选）
- klen：密码长度（可选）
- cb：进度回调函数指针（可选）
- 返回值：成功返回1，失败返回0
RSA* PEM_read_RSA_PUBKEY(FILE* fp, RSA** rsa, pem_password_cb* cb, void* u)：从PEM格式的文件中读取RSA公钥。
- fp：文件指针，指向要读取的文件
- rsa：指向RSA对象的指针的指针
- cb：密码回调函数指针（可选）
- u：密码回调函数参数（可选）
  - 返回值：成功返回读取到的RSA对象，失败返回NULL
RSA* PEM_read_RSAPrivateKey(FILE* fp, RSA** rsa, pem_password_cb* cb, void* u)：从PEM格式的文件中读取RSA私钥。
- fp：文件指针，指向要读取的文件
- rsa：指向RSA对象的指针的指针
- cb：密码回调函数指针（可选）
- u：密码回调函数参数（可选）
- 返回值：成功返回读取到的RSA对象，失败返回NULL
void RSA_free(RSA* rsa)：释放RSA对象占用的内存。
- 参数：rsa：指向RSA对象的指针
- 返回值：无

RSA结构体

typedef struct rsa_st RSA;
struct rsa_st {
    // RSA版本
    int version;
    // RSA模数
    BIGNUM* n;
    // 公钥指数
    BIGNUM* e;
    // 私钥指数
    BIGNUM* d;
    // p和q是RSA的两个素数因子之一
    BIGNUM* p;
    BIGNUM* q;
    // d mod (p-1)
    BIGNUM* dmp1;
    // d mod (q-1)
    BIGNUM* dmq1;
    // q^-1 mod p
    BIGNUM* iqmp;
    // RSA方法
    const RSA_METHOD* meth;
    // RSA引擎
    ENGINE* engine;
    // ...
};

BIGNUM结构体

BIGNUM结构体是OpenSSL库中进行RSA、DSA、ECC等非对称加密算法所必需的数据结构之一。它提供了一种方便的方式来处理大数运算，如大数的加法、减法、乘法、除法、取模等操作。

需要注意的是，在使用BIGNUM结构体时，我们需要进行适当的内存管理和错误处理，以确保安全和正确的大数运算。

typedef struct bignum_st BIGNUM;
struct bignum_st {
    BN_ULONG* d;    // 存储大数的数据
    int top;        // 大数的有效二进制位数
    int dmax;       // 数组d的最大长度
    int neg;        // 标志位，表示大数的符号（正/负）
    int flags;      // 标志位，用于控制大数的行为
};
//在不同的平台上，BN_ULONG的大小可能会有所不同。通常情况下，BN_ULONG被定义为unsigned long类型，它的大小与平台的位数相关

BIGNUM操作函数api

以下是一些常用于操作和控制大数的函数，包括加法、减法、乘法、除法、取模等运算，以及比较、赋值、转换等功能：

加法和减法：
- int BN_add(BIGNUM* r, const BIGNUM* a, const BIGNUM* b): 将大数a和b相加，结果存储在r中。
- int BN_sub(BIGNUM* r, const BIGNUM* a, const BIGNUM* b): 将大数a减去b，结果存储在r中。
乘法和除法：
- int BN_mul(BIGNUM* r, const BIGNUM* a, const BIGNUM* b, BN_CTX* ctx): 将大数a和b相乘，结果存储在r中。
- int BN_div(BIGNUM* dv, BIGNUM* rem, const BIGNUM* num, const BIGNUM* divisor, BN_CTX* ctx): 将大数num除以divisor，商存储在dv中，余数存储在rem中。
取模运算：
- int BN_mod(BIGNUM* rem, const BIGNUM* num, const BIGNUM* divisor, BN_CTX* ctx): 将大数num对divisor取模，结果存储在rem中。
比较函数：
- int BN_cmp(const BIGNUM* a, const BIGNUM* b): 比较两个大数a和b的大小，返回值为负数、零或正数，表示a小于、等于或大于b。
赋值和拷贝：
- int BN_set_word(BIGNUM* a, BN_ULONG w): 将无符号长整型数w赋值给大数a。
- BIGNUM* BN_dup(const BIGNUM* a): 复制大数a，返回一个新的BIGNUM对象。
转换函数：
- int BN_bn2bin(const BIGNUM* a, unsigned char* to): 将大数a转换为二进制格式，存储在to指向的缓冲区中。
- BIGNUM* BN_bin2bn(const unsigned char* s, int len, BIGNUM* ret): 将二进制数据s转换为大数，返回一个新的BIGNUM对象。

rsa公私钥生成案例

int main(int argc, char *argv[])
{
    //初始化openssl库
    //并不是必需的，但是建议在使用OpenSSL库进行加密操作时调用这两个函数，以确保库的正确初始化和错误处理机制的正常工作。这些函数可以提高代码的健壮性和可靠性，特别是在处理复杂的加密操作时。
    //OpenSSL_add_all_algorithms();
    //ERR_load_crypto_strings();

    RSA *rsa = RSA_new();
    //openssl中用于存储大数的数据类型BIGNUM
    //BIGNUM在RSA算法中用于存储和处理密钥和加密数据
    BIGNUM *e = BN_new();
    //RSA_F4（一个预定义的常量，通常用作RSA公钥指数）设置为BIGNUM对象e的值
    BN_set_word(e, RSA_F4);                  
    RSA_generate_key_ex(rsa, 2048, e, NULL); // 生成2048位的RSA密钥对

    // 导出公钥
    FILE *publicKeyFile = fopen("public_key.pem", "w");
    PEM_write_RSA_PUBKEY(publicKeyFile, rsa);
    fclose(publicKeyFile);

    // 导出私钥
    FILE *privateKeyFile = fopen("private_key.pem", "w");
    PEM_write_RSAPrivateKey(privateKeyFile, rsa, NULL, NULL, 0, NULL, NULL);
    fclose(privateKeyFile);

    BIO* bio = BIO_new(BIO_s_mem());

    // 将公钥写入BIO
    PEM_write_bio_RSA_PUBKEY(bio, rsa);
    char* publicKeyData;
    long publicKeyLength = BIO_get_mem_data(bio, &publicKeyData);
    printf("Public Key:\n%s\n", publicKeyData);
    
    // 清空BIO
    BIO_reset(bio);

    // 将私钥写入BIO
    PEM_write_bio_RSAPrivateKey(bio, rsa, NULL, NULL, 0, NULL, NULL);
    char* privateKeyData;
    long privateKeyLength = BIO_get_mem_data(bio, &privateKeyData);
    printf("Private Key:\n%s\n", privateKeyData);
    //释放BIO
    BIO_free(bio);
    
    //释放资源
    RSA_free(rsa);
    BN_free(e);
}

openssl生成公钥和私钥命令

# 生成私钥：这将生成一个RSA算法的私钥，并将其保存在名为private_key.pem的文件中。私钥将使用AES-256加密。
openssl genpkey -algorithm RSA -out private_key.pem -aes256
#生成公钥：这将从private_key.pem文件中提取私钥，并生成相应的公钥。公钥将保存在名为public_key.pem的文件中。
openssl rsa -pubout -in private_key.pem -out public_key.pem

openssl公私密钥使用案例

#include <openssl/rsa.h>
#include <openssl/pem.h>

// 加密函数
std::string encrypt(const std::string& plaintext, RSA* publicKey) {
    int keySize = RSA_size(publicKey);
    std::string ciphertext(keySize, '\0');

    int encryptedSize = RSA_public_encrypt(plaintext.size(), reinterpret_cast<const unsigned char*>(plaintext.data()),
                                           reinterpret_cast<unsigned char*>(ciphertext.data()), publicKey, RSA_PKCS1_OAEP_PADDING);

    if (encryptedSize == -1) {
        // 加密失败
        // 处理错误逻辑
    }

    ciphertext.resize(encryptedSize);
    return ciphertext;
}

// 解密函数
std::string decrypt(const std::string& ciphertext, RSA* privateKey) {
    int keySize = RSA_size(privateKey);
    std::string plaintext(keySize, '\0');

    int decryptedSize = RSA_private_decrypt(ciphertext.size(), reinterpret_cast<const unsigned char*>(ciphertext.data()),
                                            reinterpret_cast<unsigned char*>(plaintext.data()), privateKey, RSA_PKCS1_OAEP_PADDING);

    if (decryptedSize == -1) {
        // 解密失败
        // 处理错误逻辑
    }

    plaintext.resize(decryptedSize);
    return plaintext;
}

int main() {
    // 加载公钥
    FILE* publicKeyFile = fopen("public_key.pem", "r");
    RSA* publicKey = PEM_read_RSA_PUBKEY(publicKeyFile, nullptr, nullptr, nullptr);
    fclose(publicKeyFile);

    // 加载私钥
    FILE* privateKeyFile = fopen("private_key.pem", "r");
    RSA* privateKey = PEM_read_RSAPrivateKey(privateKeyFile, nullptr, nullptr, nullptr);
    fclose(privateKeyFile);

    std::string plaintext = "Hello, World!";

    // 加密
    std::string ciphertext = encrypt(plaintext, publicKey);

    // 解密
    std::string decryptedText = decrypt(ciphertext, privateKey);

    // 打印结果
    std::cout << "Plaintext: " << plaintext << std::endl;
    std::cout << "Ciphertext: " << ciphertext << std::endl;
    std::cout << "Decrypted Text: " << decryptedText << std::endl;

    // 释放内存
    RSA_free(publicKey);
    RSA_free(privateKey);
    return 0;
}

常见的加密算法的逆向特征

参考网址跳转

取盐算法

取盐算法，也叫摘要算法，是对数据进行一系列运算后，截取一部分关键值进行校验。因此运算过程不可逆，无法还原出加密前的初始文本。取盐算法得到的结果长度一般是固定的，无论输入的消息有多长，计算出来的消息摘要的长度总是固定的。一般地，只要输入的文本不同，对其进行摘要以后产生的摘要消息也必不相同，但相同的文本输入必会产生相同的输出。

在密码学中，盐（Salt）是指通过在密码任意固定位置插入特定的字符串，让散列后的结果和使用原始密码的散列结果不相符，这种过程称之为“加盐”。这样可以增加破解难度，提高密码安全性。

取盐算法是指如何选择盐

MD5逆向特征

字符串为 16 进制，即数字英文组合，而且英文最大是字母 f 。
位数为 16、32。
搜索关键字：

– 关键词：md5、MD5

– 默认的 key 值：0123456789abcdef、0123456789ABCDEF

– 原始MD5的魔法值（16进制）：0x67452301、0xefcdab89、0x98badcfe、0x10325476

– 原始MD5的魔法值（10进制）：1732584193、271733879、1732584194、271733878
123456 计算结果值：
16 位，结果值 49 开头。

– 16位小写计算结果：49ba59abbe56e057

– 16位大写计算结果：49BA59ABBE56E057
32 位，结果值 e10、E10 开头。

– 32位小写计算结果：e10adc3949ba59abbe56e057f20f883e

– 32位小写计算结果：E10ADC3949BA59ABBE56E057F20F883E

注意：16位的结果值是 32位的结果值的一部分。

SHA逆向特征

字符串为 16 进制，即数字英文组合，而且英文最大是字母 f
位数为 40、64、96、128 等，位数均是 8 的倍数。

//123456 计算结果值：

//SHA1：40 位：
7c4a8d09ca3762af61e59520943dc26494f8941b

//SHA256：64 位：
8d969eef6ecad3c29a3a629280e686cf0c3f5d5a86aff3ca12020c923adc6c92

//SHA384：96 位：
0a989ebc4a77b56a6e2bb7b19d995d185ce44090c13e2984b7ecc6d446d4b61ea9991b76a4c2f04b1b4d244841449454

//SHA512：128 位：
ba3253876aed6bc22d4a6ff53d8406c6ad864195ed144ab5c87621b6c233b548baeae6956df346ec8c17f5ea10f35ee3cbc514797ed7ddd3145464e2a0bab413

可还原加密算法

特征：

字符串为 16 进制，即数字英文组合，而且英文最大是字母 f 。
字符串为 base64 编码形式，由数字 0-9、小写字母 a-z、大写字母 A-Z 以及字符 +、_、= 组成，且最后一个或最后两个字符为 =。通常而言 Base64 的识别特征为索引表，当我们能找到 ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/ 这样索引表，再经过简单的分析基本就能判定是 Base64 编码。

RSA逆向特征

RSA 是典型的非对称加密，拥有一个公钥和一个私钥。

其中：
-- 客户端（浏览器）拥有公钥，服务器同时拥有公钥和私钥。
-- 同一个明文可以生成不同的密文。
-- 必须先 new JSEncrypt 加密对象，然后 setPublicKey。

加密后的数据长度不可能是 8 的倍数。
搜索关键词：new JSEncrypt、setpublickey、ABCDEFG、abcdefg。

AES逆向特征

AES 是对称加密的一种。

一般AES加密出来的数据是128 或 256 的整倍数。
搜索关键词：cryptojs.aes、encryptedString、010001（或类似二进制模值）。

DES逆向特征

搜索关键词：cryptojs.des.encrypt。

其他编码算法

Base64 逆向特征

字符串的长度为4的整数倍。
字符串的符号取值只能在 A-Z, a-z, 0-9, +, /, = 共计 65 个字符中，且 = 如果出现就必须在结尾出现。

AES算法

AES是一套对称密钥的密码术，目前已广泛使用，用于替代已经不够安全的DES算法。所谓对称密钥，就是说加密和解密用的是同一个密钥，消息的发送方和接收方在消息传递前需要享有这个密钥。和非对称密钥体系不同，这里的密钥是双方保密的，不会让任何第三方知道。

对称密钥加密法主要基于块加密，选取固定长度的密钥，去加密明文中固定长度的块，生成的密文块,与明文块长度一样。显然密钥长度十分重要，块的长度也很重要。如果太短，则很容易枚举出所有的明文-
密文映射；如果太长，性能则会急剧下降。AES中规定块长度为128 bit，而密钥长度可以选择128,192或256 bit 。暴力破解密钥需要万亿年，这保证了AES的安全性。

OpenSSL中的AES算法

头文件: <openssl/aes.h>

生成加密/解密的Key

# define AES_BLOCK_SIZE 16 // 明文分组的大小
// 加密的时候调用
int AES_set_encrypt_key(const unsigned char *userKey, const int bits, AES_KEY *key);
//- 参数userKey: 数据加密使用的原始秘钥(字符串)
//- 参数bits: 秘钥字符串占的位数
//- 参数key: 传出参数, 供后续AES api加密使用的秘钥类型

// 解密时候使用
int AES_set_decrypt_key(const unsigned char *userKey, const int bits, AES_KEY *key);
//- 参数userKey: 数据解码密使用的原始秘钥(字符串)
//- 参数bits: 秘钥字符串占的位数
//- 参数key: 传出参数, 供后续AES api解密使用的秘钥类型
//同上,成功返回0,失败返回1

参数名称	描述
userKey	16字节/24字节/32字节
bits	128bit/192bit/256bit
key	传出, 后续加解密API需要用到

加解密函数

下面使用的其实就是ECB分组模式

// 要求使用以下两个api时候参数in必须是16的整数倍, 如果不是需要将最后一组补足16字节
// 解密的时候需要将最后一个分组添加的末尾字节删除
// 加密函数
void AES_encrypt(const unsigned char *in, unsigned char *out, const AES_KEY *key);
//- 参数in: 要加密的原始数据 - 明文
//- 参数out: 传出, 加密之后 对数据 - 密文
//- 参数key: 通过AES_set_encrypt_key得到的key值

// 解密函数
void AES_decrypt(const unsigned char *in, unsigned char *out, const AES_KEY *key);
//- 参数in: 要被解密的密文
//- 参数out: 解密后得到明文
//- 参数key: AES_set_decrypt_key得到的key值

案例

int len = strlen(data); // 已经是16的整数倍
int tmpLen = 0;
char* intbuf = data;
unsigned char outbuf[1024];
while(tmpLen < len)
{
AES_encrypt(inbuf, &outbuf, key);
inbuf += 16;
outbuf += 16;
tmpLen += 16;
}
//若不是16的整数倍, 则需要在末尾进行补齐, 如何补齐呢? 在补齐的时候, 缺几个就补几, 如:
//最后的一组, 缺7个字节, 则最后都补7, xxxxxxx7777777
//如果正好是16的整数倍, 则最后需要补上16个字节(如补上一个P), 解码之后再删掉就可以了.

ECB方式加密

电子密码本模式

void AES_ecb_encrypt(const unsigned char *in, unsigned char *out,const AES_KEY *key, const int enc);
//- 参数in: 要加密/解密的数据, 长度在8字节范围就就可以
//- 参数out: 传出参数, 得到的明文/密文
//- 参数key:
//- 参数enc: 指定进行加密或者解密
	//- # define AES_ENCRYPT 1
	//- # define AES_DECRYPT 0

函数的使用方式

//这个函数调用一次只能处理8字节
while(条件)
{
	AES_ecb_encrypt();
}

CBC方式加密

密码分组链接模式

1	void AES_cbc_encrypt(const unsigned char in, unsigned char out,size_t length, const AES_KEY key,unsigned char ivec, const int enc);

参数**in**: 要加密/解密的数据
参数**out**: 通过加密得到的密文/通过解密得到的明文
参数**Length**: 修饰的是in参数
- 如果in长度(需要加上'\0'长度)是16的整数倍, 那么length就等于该长度
  
  length = strlen(in)+1; (1就是尾部的’\0’)
- in的长度(需要加上'\0'长度)不是16的整数倍, 需要将其变成16的整数倍
  
  计算当前有多少个分组 gourp = (strlen(in)+1) / 16;
  
  将最后不满16字节的分组添加进来并将其字节数填充到16字节
  1
  2
  group=group+1
  length = group * 16
参数**key**: 通过AES_set_encrypt_key得到的key值/ AES_set_decrypt_key得到的key值
参数**ivec**:
- 随机字符串, 长度和明文分组长度相同.
- 参与加解密的初始化向量的值必须相同
参数**enc**:
- # define AES_ENCRYPT 1
- # define AES_DECRYPT 0

案例

char* mykey = "0123456789abcdef";
AES_KEY key;
AES_set_encrypt_key((const unsigned char*)mykey,128,&key);
//需要加密的字符串
int length;
char *mystr = "hello world,hao are you, i am fine, thank you";
//计算第三个参数length的长度,包含了字符串末尾的\0
if((strlen(mystr) + 1)%16 == 0)
{
    //长度刚好合适
    length = strlen(mystr)+1;
}
else
{
    length = ((strlen(mystr) + 1)/16 +1)*16;
}
unsigned char* encrypt = (unsigned char*)calloc(length,1);
unsigned char iv[16];
memset(iv,'a',sizeof(iv));
for (int i = 0; i < 16; i++)
{
    std::cout<<"iv["<<i<<"]==["<<iv[i]<<"]"<<std::endl;
}
AES_cbc_encrypt((const unsigned char*)mystr,encrypt,length,&key,iv,AES_ENCRYPT);
std::cout<<"===================="<<std::endl;
for (int i = 0; i < 16; i++)
{
    std::cout<<"iv["<<i<<"]==["<<iv[i]<<"]"<<std::endl;
}
cout<<"加密后内容为:"<<encrypt<<endl;
std::cout<<"===================="<<std::endl;
std::cout<<"下面是解密"<<std::endl;
std::cout<<"===================="<<std::endl;
AES_set_decrypt_key((const unsigned char*)mykey,128,&key);
memset(iv,'a',sizeof(iv));
unsigned char *decrypt = (unsigned char*)calloc(length,1);
AES_cbc_encrypt(encrypt,decrypt,length,&key,iv,AES_DECRYPT);
 for (int i = 0; i < 16; i++)
{
    std::cout<<"iv["<<i<<"]==["<<iv[i]<<"]"<<std::endl;
}
std::cout<<"解密后的内容为:"<<decrypt<<std::endl;
return 0;

输出为:

iv[0]==[a]
iv[1]==[a]
iv[2]==[a]
iv[3]==[a]
iv[4]==[a]
iv[5]==[a]
iv[6]==[a]
iv[7]==[a]
iv[8]==[a]
iv[9]==[a]
iv[10]==[a]
iv[11]==[a]
iv[12]==[a]
iv[13]==[a]
iv[14]==[a]
iv[15]==[a]
====================
iv[0]==[r]
iv[1]==[8]
iv[2]==[V]
iv[3]==[]
iv[4]==[]
iv[5]==[�]
iv[6]==[�]
iv[7]==[a]
iv[8]==[_]
iv[9]==[~]
iv[10]==[�]
iv[11]==[�]
iv[12]==[]
iv[13]==[�]
iv[14]==[]]
iv[15]==[�]
加密后内容为:T��h�u�f�{&y�]&�7�h���(���
                                       n�pr8V��a_~���]�
====================
下面是解密
====================
iv[0]==[r]
iv[1]==[8]
iv[2]==[V]
iv[3]==[]
iv[4]==[]
iv[5]==[�]
iv[6]==[�]
iv[7]==[a]
iv[8]==[_]
iv[9]==[~]
iv[10]==[�]
iv[11]==[�]
iv[12]==[]
iv[13]==[�]
iv[14]==[]]
iv[15]==[�]
解密后的内容为:hello world,hao are you, i am fine, thank you

单向散列函数

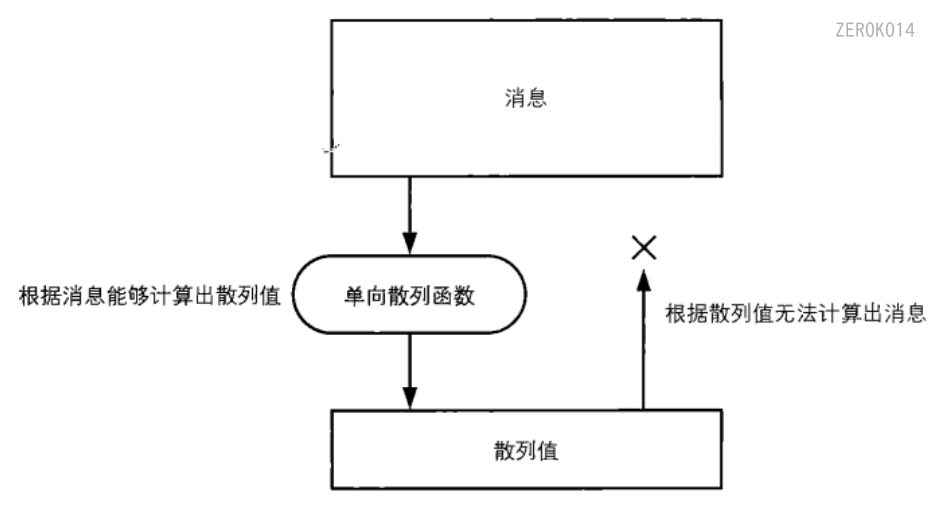
用于获取消息的**”指纹”**

单向散列函数（one-wayftnction）有一个输入和一个输出，其中输入称为消息（message），输出称为散列值（hashvalue）。单向散列函数可以根据消息的内容计算出散列值，而散列值就可以被用来检查消息的完整性。

单向散列函数也称为消息摘要函数（message digest function）、哈希函数或者杂凑函数。
单向散列函数输出的散列值也称为消息摘要（message digest）或者指纹（fifingerprint）。
完整性也称为一致性。

哈希函数特点

压缩性 : 任意长度的数据，算出的值长度都是固定的
容易计算 : 计算散列值所花费的时间必须要短。尽管消息越长，计算散列值的时间也会越长，但如果不能在现实的
时间内完成计算就没有意义了。
抗修改性 : 对原数据进行任何改动，哪怕只修改1个字节，所得到的值都有很大区别
强抗碰撞性 : 已知原数据和其哈希值，想找到一个具有相同哈希值的数据（即伪造数据）是非常困难的
单向性（不可逆）

哈希函数的应用

检测软件是否被篡改

我们可以使用单向散列函数来确认自己下载的软件是否被篡改。很多软件，尤其是安全相关的软件都会把通过单向散列函数计算出的散列值公布在自己的官方网站上。用户在下载到软件之后，可以自行计算散列值，然后与官方网站上公布的散列值进行对比。通过散列
值，用户可以确认自己所下载到的文件与软件作者所提供的文件是否一致。这样的方法，在可以通过多种途径得到软件的情况下非常有用。为了减轻服务器的压力，很多软件作者都会借助多个网站（镜像站点）来发布软件，在这种情况下，单向散列函数就会在检测软件是否被篡改方面发挥重要作用。

消息认证码

使用单向散列函数可以构造消息认证码。
消息认证码是将“发送者和接收者之间的共享密钥”和“消息，进行混合后计算出的散列值。使用消息认证码可以检测并防止通信过程中的错误、篡改以及伪装

对于发送端:

将要发送的数据进行哈希运算, 参与运算的数据是: 原始数据+秘钥, 可以得到一个散列值
将散列值与原始数据进行拼接, 一起发送给对方;

对于接收端:

接收对方发来的数据, 并将原始数据和散列值拆分开, 得到散列值和原始数据
对原始数据进行哈希运算: 参与运算的数据也是:原始数据+秘钥, 可以得到一个散列值
将计算得到的散列值与接受到的散列值进行比较, 相同则认为没有被篡改, 否则认为被篡改了.

注意: 发送方和接受方使用的秘钥是同一个秘钥(对称秘钥,秘钥分发困难), 这个秘钥只有发送方和接受方知道,
若这个秘钥被第三方知道了, 就没有办法保证数据的是安全的了

数字签名

在进行数字签名时也会使用单向散列函数。
数字签名是现实社会中的签名（sign）和盖章这样的行为在数字世界中的实现。数字签名的处理过程非常耗时，因此一般不会对整个消息内容直接施加数字签名，而是先通过单向散列函数计算出消息的散列值，然后再对这个散列值施加数字签名。

使用的是非对称加密, 有公钥和私钥

数字签名流程:

A将明文进行哈希运算得到一个散列值, 并且用私钥对哈希值进行加密, 然后将明文和加了密的哈希值一起发送给B;
B收到之后, 使用公钥对哈希值进行解密, 得到原始的哈希值, 并且对明文进行哈希运算也得到一个哈希值, 最后对自己生成的哈希值和A发送过来的哈希值进行比较, 如果一样, 则认为没有被篡改.

使用数字签名的目的是为了不可抵赖性.(表明拿私钥的一方发送的数据, 是不可抵赖的)

一次性口令或登录验证

一次性口令

使用单向散列函数可以构造一次性口令（one-time password）。
一次性口令经常被用于服务器对客户端的合法性认证。在这种方式中，通过使用单向散列函数可以保证口令只在通信链路上传送一次（one-time），因此即使窃听者窃取了口令，也无法使用。

登录验证

当用户登录的时候, 需要输入密码, 这个密码会经过加密运算, 经过运算之后的值再与服务器中保存的密码进行比较, 若相同则输入密码正确, 允许登录.
若用户忘记密码, 则只能重置密码, 服务端并不知道用户原来的明文, 只能是重新设置

常用的哈希函数

Md4/Md5

MD4是由Rivest于1990年设计的单向散列函数，能够产生==128比特==的散列值（RFC1186，修订版RFC1320）。不过，随着Dobbertin提出寻找MD4散列碰撞的方法，因此现在它已经不安全了。
MD5是由Rwest于1991年设计的单项散列函数，能够产生==128比特==的散列值（RFC1321）。
MD5的强抗碰撞性已经被攻破，也就是说，现在已经能够产生具备相同散列值的两条不同的消息，因此它也已经不安全了。
MD4和MD5中的MD是消息摘要（Message Digest）的缩写。

SHA-1/SHA-256/SHA-384/SHA-512

SHA-1是由NIST（National Institute Of Standardsand Technology，美国国家标准技术研究所）设计的一种能够产生==160比特==的散列值的单向散列函数。1993年被作为美国联邦信息处理标准规格（FIPS PUB 180）发布的是SHA,1995年发布的修订版FIPS PUB 180-1称为SHA-1。
SHA-1的消息长度存在上限，但这个值接近于2^64^比特，是个非常巨大的数值，因此在实际应用中没
有问题。
SHA-256、SHA-384和SHA-512都是由NIST设计的单向散列函数，它们的散列值长度分别为==256比特==、==384==比特和==512比特==。这些单向散列函数合起来统称SHA-2，它们的消息长度也存在上限（SHA-256的上限接近于 2^64^ 比特，SHA-384 和 SHA-512的上限接近于 2^128^ 比特）。这些单向散列函数是于2002年和 SHA-1 一起作为 FIPS PUB 180-2发布的 SHA-1 的强抗碰撞性已于2005年被攻破, 也就是说，现在已经能够产生具备相同散列值的两条不同的消息。不过，SHA-2还尚未被攻破

哈希函数	散列值长度(bit)	散列值长度(byte)
Md4/Md5	128bit	16byte
SHA-1	160bit	20byte
SHA-224	224bit	28byte
SHA-256	256bit	32byte
SHA-384	384bit	48byte
SHA-512	512bit	64byte

最终需要对得到的散列值做转换, 以16进制格式的字符串表

openssl库中哈希函数用法

头文件位置(-I) openssl根目录/include/openssl/

库文件位置(-L) openssl根目录/lib

win下添加附加依赖项:libcrypto.lib和libssl.lib (无法解析的外部符号报错)

linux下添加附加依赖项: -lssl -lcrypto

// 第一种方式(第二种方式为第一种方式的封装)
// 初始化一个MD5_CTX类型的变量
int MD5_Init(MD5_CTX *c);
- c: 传出
// 给哈希函数添加要运算的数据
int MD5_Update(MD5_CTX *c, const void *data, size_t len);
- C: 传入
- data: 传入, 要进行哈希运算的数据
- len: data参数的长度
文件1G
while(read(fd, buf, len))
{
MD5_Update(c, buf, buflen);
}
// 计算结果
int MD5_Final(unsigned char *md, MD5_CTX *c);
- md传出参数, 需要将计算出的散列值保存到md中
- c: 出入
//=========================================
// 第二种方式
unsigned char *MD5(const unsigned char *d, size_t n, unsigned char *md);
- d: 要进行哈希运算的字符串
- n: 第一个参数的长度
- md: 计算出的散列值
返回值:
得到的散列值
//===========================================================================
int SHA1_Init(SHA_CTX *c);
int SHA1_Update(SHA_CTX *c, const void *data, size_t len);
int SHA1_Final(unsigned char *md, SHA_CTX *c);
unsigned char *SHA1(const unsigned char *d, size_t n, unsigned char *md);
//上述几个函数的用法同md5的几个函数.

相关的函数说明可以在openssl安装目录中去查看:

C:\OpenSSL-Win32\include\openssl, 如md5.h和sha.h
能够用到的库名: libssl.lib libcrypto.lib
使用到的库所在的路径: C:\OpenSSL-Win32\lib
使用到的头文件所在的路径: C:\OpenSSL-Win32\include

注意: 在使用vs进行项目开发的时候, 需要指定头文件所在路径和库文件所在路径

可以用诸如md5sum+文件路径命令(xxxsum)直接计算得出md5值

sha1简单案例

下面案例为vs下,需指定头文件所在路径和库文件所在路径以及添加依赖项

#define _CRT_SECURE_NO_WARNINGS
#include <openssl/sha.h>
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
int main()
{
		unsigned char md[SHA_DIGEST_LENGTH];
		unsigned char md1[SHA_DIGEST_LENGTH*2+1];
		const char* p = "你好, 世界";
		SHA1((unsigned char*)p, strlen(p) + 1, md);
		//cout << "sha1: " << md << endl; //若有不可见或者		是二进制数据, 使用cout会出现bug
		// 将散列值转换为16进制格式的字符串
		// base64
		for (int i = 0; i < SHA_DIGEST_LENGTH; ++i)
		{
				// 将每个字符格式化010203
				sprintf((char*)&md1[i*2], "%02x", md[i]);
		}
		cout << "sha1: " << md1 << endl;
		return 0;
}

hmac简单案例

//下面例子其实也是使用sha1的单向散列方式
#include <iostream>
using namespace std;
#include <string>
#include <stdlib.h>
#include "openssl/hmac.h"
#include "openssl/sha.h"

int main(int argc, char *argv[])
{
    HMAC_CTX *ctx = HMAC_CTX_new();
    char key[] = "";//密钥
    unsigned char data[] = "";//要单向散列的数据
    unsigned char md[SHA_DIGEST_LENGTH];//单向散列输出的结果
    char mdBuf[SHA_DIGEST_LENGTH * 2 + 1] = {0}; // 一个字节用两个字符来表示,因此乘2,该变量用于打印
    //HMAC_Init(ctx, key, strlen(key), EVP_sha1());//这个也可以代替下面那行
    HMAC_Init_ex(ctx, key, strlen(key), EVP_sha1(),NULL);//设置sha1单向散列函数
    HMAC_Update(ctx, data, strlen((const char *)data));
    int len = SHA_DIGEST_LENGTH;
    HMAC_Final(ctx, md, (unsigned int *)&len); // 哈希结果输出到md中
    for (int i = 0; i < SHA_DIGEST_LENGTH; i++)
    {
        sprintf(&mdBuf[i * 2], "%02x", md[i]);
    }
    std::cout << mdBuf << std::endl;
    // 下面是第二种方式
    memset(md, 0, sizeof(md));
    // 一行代码生成结果
    HMAC(EVP_sha1(), key, strlen(key), data, strlen((const char *)data), md, (unsigned int *)&len);
    for (int i = 0; i < SHA_DIGEST_LENGTH; i++)
    {
        sprintf(&mdBuf[i * 2], "%02x", md[i]);
    }
    std::cout << mdBuf << std::endl;
    return 0;
}

base64编码

Base64是一种基于64个可打印字符来表示二进制数据的表示方法.在Base64中的可打印字符包括字母A-Z,a-z,数字0-9,这样共有62个字符,此外两个可打印符号在不同的系统中而不同

只是一种编码格式,并不用于加密,因为特征明显且易于还原

为什么要使用base64:

在计算机中任何数据都是按ascii码存储的,而ascii码的128-255之间的值是不可见字符.而在网络上交换数据时,比如说从A地传到B地,往往要经过多个路由设备,由于不同的设备对字符的处理方式有一些不同,这样那些不可见字符就有可能被处理错误,这是不利于传输的.所以就先把数据先做一个Base64编码,统统变成可见字符,这样出错的可能性就大大降低了

base64的主要应用场景

作为电子邮件的传输编码

邮件传输协议只支持ASCII字符传递,因此如果要传输二进制文件,如:图片,视频需要通过base64编码.
Http协议

HTTP协议要求请求行和请求头都必须是ASCII编码
数据库数据读写 - blob(big large object)

存储二进制的大数据块

将中文传入不支持中文的数据库

具体算法:

把 3 个 8 位字节 (3*8=24) 转换为 4 个 6 位字节 (4*6 个字节)
把 6 位的前面补两个 0, 形成 8 位一个字节的形式
如果剩下的字符不足 3 个字节, 则用 0 填充, 输出字符使用 ‘=’ ,因此编码后输出的文本末尾可能会出现 1 个或 2 个 ‘=’, 表示补了多少字节, 解码的时候会自动去掉

[[QT#QT 的 base 64 编码|QT 的 base 64 编码]]

安全传输

非对称加密好是好,但一般由于加解密太废时间了,导致卡顿,因此实际上都只使用非对称加密参与流程获得对称密钥,在使用对称密钥来进行双方的通信.对称加密有硬件加速,现代CPU都内置AES指令集.

参考HTTPS加密进化的动画解说

密钥协商

图示:

注意实际的情况中,r1与r2的发送流程应该是使用非对称加密算法的公钥来加密后发送的,只有服务器的私钥才能解开,此案例中直接明文发送了

这样也无法高枕无忧,因为无法确定公钥一定是服务器的,害怕被冒充,所以同样需要效仿https实现证书机制,至于证书的签发机构是不是受信任?因为受信任机构的根证书被安装到了系统中.即使有证书机制,还是要防范假的根证书被安装到了系统

客户端协商流程

客户端生成一个随机数r1,同时使用openssl中哈希函数对r1进行哈希运算,得到一个哈希值
将要发送的数据进行编码
发送数据给服务端(包含r1和对应的哈希值)
客户端等待接受服务端的应答
{服务端协商流程操作}
对接收到的数据进行解码
判断rv的值,若rv为-1表示生成密钥失败
如果成功;rv = 0;

获得服务端发来的随机字符串r2,将r2和r1进行拼接进行哈希运算得到一个新的**seckey1**
客户端将密钥信息写入共享内存

服务端协商流程

收到请求数据之后,首先解码
根据客户端ID+服务端ID查询数据库,校验客户端是否合法,如不合法直接拒绝服务
服务端校验r1消息认证码

使用和客户端相同的算法生成哈希值,然后将这个哈希值与接收到的哈希值做比较

如果不一样,则拒绝服务,如果一样,则继续后续操作
服务端也生成随机数r2
服务端将r1和r2进行拼接,然后使用与客户端相同的哈希算法进行哈希运算,得到一个哈希值,这个哈希值就当做新的密钥**seckey2**
将新的密钥信息写入共享内存和数据库
服务端发送应答信息给客户端;

密钥校验

客户端

客户端将密钥进行哈希运算,得到一个哈希值
将哈希值发送给服务端

服务端

收到哈希值,自己也生成一个哈希值
将两个哈希值进行比较,相同则密钥协商成功,否则秘钥协商失败

密钥注销

客户端

将clientID,serverID和密钥ID发送给服务端

服务端

服务端收到请求之后,将共享内存和数据库中的密钥的状态修改为不可用状态

安全传输平台结构

TcpClient TcpServer tcp通信操作的封装(完全可以封装到一个类中) (内部处理了超时问题)

ShareMemory 实现最基本的共享内存操作
SecKeyShm 对共享内存操作的进一步封装

ServerOperation 服务器的操作封装
ClientOperation 客户端的操作封装

BaseASN1 实现最基本的ASN1编码逻辑
SequenceASN1 ASN1编码的进一步封装
Codec 对为了实现对不同结构体的ASN1编码而对SequenceASN1做的进一步封装的一个用于实现多态的基类
RequestCodec和RespondCodec 用于具体实现Codec多态的[对请求数据进行ASN1编码的类型]以及[对回应数据进行ASN1编码的类型]
FactoryCodec 生产各种工厂的抽象类,其生产工厂的函数返回的类型为Codec(多态对多态)
RequestFactory和RespondFectory 具体的[生产请求数据的工厂的类]和[生产回应数据的工厂的类]

Mysqlop 对mysql操作的封装
ItcastLog 实现日志功能

根证书比对工具

开源工具下载

根证书相关知识