算法
算法
ZEROKO14算法是指解决问题的方法(或过程),是若干指令的有穷序列
算法的本质就是「穷举」
算法的本质都是穷举二(多)叉树,有机会的话通过剪枝或者备忘录的方式减少冗余计算,提高效率
利用计算机的速度,解决现实中的抽象问题
穷举要做到两点
- 无遗漏
- 无冗余
遗漏会导致算法错误,冗余会拖慢算法运行速度
算法的难点在于两类问题
如何穷举(递归算法往往解决的是这类问题)
如何聪明的穷举
比如后文 Union Find 并查集算法详解,告诉你一种高效计算连通分量的技巧,理论上说,想判断两个节点是否连通,用DFS/BFS 暴力搜索(穷举)肯定可以做到,但人家 Union Find 算法硬是用数组模拟树结构,给你把连通性相关的操作复杂度给干到
O(1)了。
再比如贪心算法技巧,所谓贪心算法就是在题目中发现一些规律(专业点叫贪心选择性质),使得你不用完整穷举所有解就可以得出答案。
动态规划好歹是无冗余地穷举所有解,然后找一个最值,贪心算法倒好,都不用穷举所有解就可以找到答案,所以后文贪心算法解决跳跃游戏 中贪心算法的效率比动态规划还高。
再比如大名鼎鼎的KMP算法,KMP 算法的本质是聪明地缓存并复用一些信息,减少了冗余计算,后文 KMP 字符匹配算法 就是使用计算机的思路实现的 KMP 算法。
顺便强调下,「算法工程师」做的这个「算法」,和「数据结构与算法」中的这个「算法」完全是两码事
对前者来说,重点在数学建模和调参经验,计算机真就只是拿来做计算的工具而已;而后者的重点是计算机思维,需要你能够站在计算机的视角,抽象、化简实际问题,然后用合理的数据结构去解决问题。
所以,你千万别以为学好了数据结构和算法就能去做算法工程师,也不要以为只要不做算法工程师就不需要学习数据结构和算法。坦白说,大部分开发岗位工作中都是基于现成的开发框架做事,不怎么会碰到底层数据结构和算法相关的问题,但另一个事实是,只要找技术相关的岗位,数据结构和算法的考察是绕不开的,因为这块知识点是公认的程序员基本功。
为了区分,不妨称算法工程师研究的算法为「数学算法」,称刷题面试的算法为「计算机算法」,此篇内容主要聚焦的是「计算机算
法」。「计算机算法」的思维恰恰相反:有没有什么数学公式就交给你们人类去推导吧,如果能找到一些巧妙的定理那最好,但如果找不
到,那就穷举呗,反正只要复杂度允许,没有什么答案是穷举不出来的
算法入门
时间复杂度

时间复杂度是衡量算法执行时间的一个指标,它表示算法运行时间随输入规模增长的趋势。通常使用大O符号表示,描述算法在输入规模增大时的渐进行为。
举个例子,冒泡排序算法的时间复杂度是 $O(n^2)$,这意味着算法的运行时间与输入规模的平方成正比。也就是说,当输入规模翻倍时,算法的运行时间会变为原来的四倍。
时间复杂度可以有多种不同的衡量方式。一种常见的方式是计算算法执行的操作次数。另一种方式是测量算法在特定计算机上运行所需的时间。
时间复杂度在算法设计中非常重要,因为它可以帮助确定算法的效率。时间复杂度较高的算法可能不适用于大规模数据集,因为它们可能需要太长的运行时间。
有许多技巧可以改善算法的时间复杂度。一种常见的方法是使用分治策略,将问题分解为更小的子问题,以便更高效地解决。另一种方法是使用动态规划,将子问题的结果存储起来,避免重复计算。
时间复杂度是一个复杂的主题,没有一种通用的方法适用于所有算法。然而,通过了解不同的时间复杂度衡量方式,并使用适当的技巧改善算法的时间复杂度,可以设计出适用于各种问题的高效算法。
常数时间的操作:一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作
时间复杂度为一个算法流程中,常数操作数量的一个指标。常用O(读作big O)来表示。具体来说,先要对一个算法流程非常熟悉,然后去写出这个算法流程中,发生了多少常数操作,进而总结出常数操作数量的表达式。
表达式中,只要高阶项,不要低阶项的系数(阶:未知数的次方数),剩下的部分如果为f(N),那么时间复杂度为O(f(N))。
【评价一个算法流程的好坏】:先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是“常数项时间”。
空间复杂度
与时间复杂度相似,但针对空间
算法概述
- 递归与分治Divide and Conquer
- 动态规划Dynamic Programming
- 贪心算法Greedy
- 回溯算法Backtrack
- 分支限界法Branch and Bound
- 随机算法
- 近似算法
算法第一步是问题建模
问题建模
问题类型:
- 计数问题
- 构造问题
- 判定问题(二元的,yes or no)
- 最优化问题
问题建模:
- 输入
input:定义问题空间(即特定对象集合) - 输出
output:定义解空间 - 约束
constraint:定义约束函数 - 目标
objective function:定义目标函数
问题实例:instance of a problem:问题模型的实例化,即一个给定输入的实际问题
图灵机
1936年,Alan M. Turing (1912-1954)提出了一种在理论计算机科学中广泛采用的抽象计算机
它是通用数字计算机的理论原型。图灵机可制造出一种十分简单但计算能力极强的计算机装置。
用有限的指令和有限的存储空间可算尽一切可算之物。
一台图灵机是一个七元组
图灵机=有限状态自动机+无限纸带 => 算尽一切可算之物
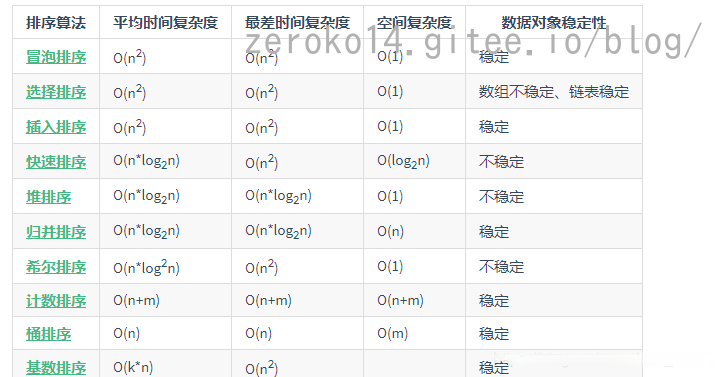
排序算法
- 概念
排序是计算机内经常进行的一种操作,其目的是将一组“无序”的数据元素调整为“有序”的数据元素。
- 排序数学定义:
假设含n个数据元素的序列为{ R1, R2, …, Rn},其相应的关键字序列为{ K1, K2, …, Kn}这些关键字相互之间可以进行比较,即在它们之间存在着这样一个关系 :
Kp1≤Kp2≤…≤Kpn
按此固有关系将上式记录序列重新排列为{ Rp1, Rp2, …,Rpn}的操作称作排序
- 排序的稳定性
如果在序列中有两个数据元素r[i]和r[j],它们的关键字k[i] == k [j],且在排序之前,对象r[i]排在r[j]前面。如果在排序之后,对象r[i]仍在r[j]前面,则称这个排序方法是稳定的,否则称这个排序方法是不稳定的。

- 内排序和外排序
- 内排序:在排序过程中,待排序的所有记录全部都放置在内存中,排序分为:内排序和外排序。
- 外排序:由于排序的记录个数太多,不能同时放置在内存,整个排序过程需要在内外存之间多次交换数据才能进行。
- 排序的审判
- 时间性能:关键性能差异体现在比较和交换的数量
- 辅助存储空间:为完成排序操作需要的额外的存储空间,必要时可以“空间换时间”
- 算法的实现复杂性:过于复杂的排序法会影响代码的可读性和可维护性,也可能影响排序的性能
- 总结
- 排序是数据元素从无序到有序的过程
- 排序具有稳定性,是选择排序算法的因素之一
- 比较和交换是排序的基本操作
- 多关键字排序与单关键字排序无本质区别
- 排序的时间性能是区分排序算法好坏的主要因素
其他的一些排序算法:
- 快速排序(Quick Sort):快速排序是一种基于分治思想的排序算法,通过选择一个基准元素,将数组分为两个子数组,并递归地对子数组进行排序。快速排序的平均时间复杂度为O(nlogn),在大多数情况下具有较高的效率。(快速排序与下文的排序算法不是一个东西)
- 归并排序(Merge Sort):归并排序也是一种分治算法,它将数组递归地分成两个子数组,然后将两个有序子数组合并成一个有序数组。归并排序的时间复杂度为O(nlogn),并且具有稳定性。
- 堆排序(Heap Sort):堆排序利用堆这种数据结构进行排序,通过构建最大堆或最小堆来实现排序。堆排序的时间复杂度为O(nlogn),并且具有原地排序的特点。
需要注意的是,这些算法的性能取决于输入数据的规模和特征。对于小规模的数据集,简单的排序算法如插入排序和冒泡排序可能更高效。对于已经部分有序的数据集,插入排序和冒泡排序也可能比其他算法更快。
C++标准库中的std::sort函数使用了一种高效的排序算法(通常是快速排序或归并排序)
冒泡排序
时间复杂度是$O(n^2)$
- 冒泡排序是一种效率低下的排序方法,在数据规模很小时,可以采用。数据规模比较大时,最好用其它排序方法。
- 上述例子对冒泡做了优化,添加了flag作为标记,记录序列是否已经有序,减少循环次数。
选择排序
时间复杂度是$O(n^2)$

插入排序
插入排序算法是一种简单的排序算法,也成为直接插入排序算法。它是一种稳定的排序算法,对局部有序的数据具有较高的效率。
插入排序算法是一个队少量元素进行排序的有效算法。比如,打牌是我们使用插入排序方法最多的日常生活例子。我们在摸牌时,一般会重复一下步骤。期初,我们手里没有牌,摸出第一张,随意放在左手上,以后每一次摸排,都会按照花色从小到大排列,直到所有的牌摸完。插入排序算法采用的类似思路,每一次从无序序列中拿出一个数据,将它放到已排序的序序列的正确位置,如此重复,直到所有的无序序列中的数据都找到了正确位置。
插入排序(Insertion Sort)的时间复杂度是$O(n^2)$。在最坏的情况下,需要比较和移动元素的次数是n(n-1)/2次,其中n是待排序数组的长度。
快速排序
时间复杂度为O(nlogn)
下面代码是使用交换法实现的快排
1 | void quickSort(int arr[],int left,int right) |
归并排序
时间复杂度为O(nlogn)
堆排序
时间复杂度为O(nlogn)
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
基本思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。
倒序对每个父节点进行下潜操作,通过这个操作使得混乱数组具备堆序性,如下流程

反复调用pop_heap函数来实现,每次将最大元素移动到范围的末尾,就可以实现堆排序
pop_heap函数的实现参考下面流程:

[[数据结构#堆|堆的详解点击跳转]]
[[stl#堆相关算法|stl中也有提供各种现成函数]]
计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
① 找出待排序的数组中最大和最小的元素
② 统计数组中每个值为i的元素出现的次数,存入数组C的第i项
③ 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
④ 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1

平均时间复杂度:O(n + k)
最佳时间复杂度:O(n + k)
最差时间复杂度:O(n + k)
空间复杂度:O(n + k)
随眠排序
遍历数组,对每个元素创建一个新线程,该线程休眠的时间与元素的值成正比
将排序任务委托给了CPU的调度器…
查找算法
二分查找
无重复元素 的 升序 排列数组中的插入查找
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
1 | int searchInsert(vector<int> &nums, int target) |
- 时间复杂度:O(logn),其中 n 为数组的长度。二分查找所需的时间复杂度为 O(logn)
- 空间复杂度:O(1)。我们只需要常数空间存放若干变量
字符串匹配算法
KMP算法
一种改进的字符串匹配算法,利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的,将时间复杂度从O(m*n)变成O(m+n)
next数组含义为存放子串对应下标前存在的最长相等前后缀的长度(相等前后缀不能是字符串本身)
生成next数组函数
[递推思维]: 通过已经掌握的信息,来避免进行重复的运算
1 | //生成next数组(next数组含义为存放子串对应下标前存在的最长相等前后缀的长度) |
更简洁的版本
任何位置匹配到的同时+1,就继续匹配下一个,同时把当前匹配的数量写入next[i+1]
1 |
|
kmp搜索函数
借助于next数组
1 | int kmpSearch(char* str,char* subStr) |
BM算法
Boyer-Moore字符串搜索算法
字符串匹配BM算法,全称是Boyer-Moore算法,其核心思想是:在模式串中某个字符与主串不能匹配的时候,将模式串往后多滑动几位,以此提高匹配的效率
为了能够一次性多滑动几位,在真正进行字符串匹配之前,先进行了一系列预处理操作,遵循 坏字符规则 和 好后缀规则
坏字符规则
按模式串倒序匹配的过程中,把匹配失败时主串中的字符,叫做坏字符,然后在模式串中查找坏字符,若找到匹配字符,则将模式串中的匹配字符和坏字符对齐,否则直接将模式串滑动到坏字符之后的一位,再重复进行上述过程.
把坏字符在模式串中的位置记为 si 值,如果 坏字符 在 模式串 中存在,将坏字符在模式串中的下标记作 xi 值,若不存在 xi 记作 -1,移动的位数就等于 si-xi 值。
把坏字符在模式串中的位置记为 si 值,如果 坏字符 在 模式串 中存在,将坏字符在模式串中的下标记作 xi 值,若不存在 xi 记作 -1,移动的位数就等于 si-xi 值。
注意:单纯采用坏字符的策略,计算出来的移动位数有可能是负数,因此 BM 算法还需要使用好后缀规则来避免这种情况。因此,在该算法中可以省略坏字符规则,却不能省略好后缀规则。
好后缀规则
按模式串 倒序匹配 过程中,失配点之后模式串中 匹配成功的那段字符-U ,为好后缀。好后缀规则在于,考虑能否根据 已经匹配成功 的字符,直接推算出下次移动的位置。
理论依据:如果
好后缀-U在模式串找不到 另一个 匹配子串,只要U-整体还参与匹配,就肯定无法匹配,因为已经确定模式串中没有与和U-整体相同的字符串。但若U-的部分后缀和模式串的前缀有 重合 且相等,则有可能会完全匹配。
上图是 只 基于 好后缀规则 的匹配过程,涉及 后缀整体匹配 和 后缀子串和模式串前缀 的匹配。而下图则是 坏字符+好后缀 两种规则的匹配方式,具体选哪种取决于可移动的最大距离。
Sunday算法
Sunday算法实际上是一种对BM算法的改进,其基本思路与BM算法相似。但是与BM算法不同的是,Sunday算法的比较是从模式串的开头进行比较的,并且Sunday算法在不匹配情况发生时,模式串跳转的幅度更大,所以从这一点上来说,Sunday算法的效率甚至比BM算法更高。
原理
从左到右比对,当发现比对失败时候(w),观察与模式串对齐的最后一位字符的下一位字符(本例中就是文本串中的D)是否出现在模式串中。
这一做法的意图是:如果文本串中,与模式串对齐位置上的下一位字符,也就是文本串中的D并没有出现在文本串中的话,那么就可以确定,从失配字符W向后,一直到字符D中间的这段内容与模式串肯定是不可能匹配了,所以我们可以直接跳过这段内容,直接将模式串跳转到字符D后面的位置进行对齐,然后重新开始比较。

依然以上图为例,在进行模式串跳转之后,我们发现文本串中的_与模式串中的F首先就是不匹配的:
但是此时在文本串中,与模式串对齐的下一位字符T在模式串中出现过:

此时,我们将与模式串对齐的下一位字符与模式串中出现的位置对齐,然后继续进行比较:

编码
坏字表:记录了是否有某个字符(-1表示没有该字符),又记录了字符最后出现的位置.
1 | int sunday(const char *text, const char *pattern) { |
该算法也常用于特征码查询.(下面代码为转载,未测试)
1 |
|
多种算法间的比较
KMP算法:
适用于需要频繁匹配的场景,能够保证线性时间复杂度。
BM算法:
在处理较长模式串或较大的字母表时表现较好,适合于文本中出现模式串较少的情况。
Sunday算法:
通常在实际应用中表现得更快,适合于大多数字符串匹配场景,尤其是当模式串较短时。
贪心算法
贪心算法,又称贪婪法,是寻找最优解问题的常用方法。这种方法模式一般将求解过程分成若干个步骤,但每个步骤都应用贪心原则,选取当前状态下最好或最优的选择(局部最有利的选择),并以此希望最后堆叠出的结果也是最好或最优的解。
这就好像一个贪婪的人,他事事都想要眼前看到最好的那个,看不到长远的东西,也不为最终的结果和将来着想,贪图眼前局部的利益最大化,有点走一步看一步的感觉。
例如,假设你开了间小店,不能电子支付,钱柜里的货币只有25分、10分、5分和1分四种硬币,如果你是售货员且要找给客户41分钱的硬币,如何安排才能找给客人的钱既正确且硬币的个数又最少?这就是一个典型的贪心算法的应用场景。
然而,贪心算法不能保证最后求得的解是最优的,同时,贪心算法只能求满足某些约束条件的可行解的范围。如果一个问题的最优解只能用蛮力法穷举得到,则贪心法不失为寻找问题近似最优解的一种较好的方法。贪心算法的时间复杂度通常比较低,但不一定能够得到全局最优解。
总的来说,贪心算法是一种基于贪心策略的算法,它在每一步选择中都采取在当前状态下最好或最优的选择,从而希望导致结果是最好或最优的。贪心算法通常适用于求解最优化问题,如最小生成树、最短路径、背包问题等
排列组合公式
记忆有点模糊,故写在此处以做温习
排列组合公式推导:
排列公式
排列需要考虑顺序
Arrangement 排列 或 Permutation 排列
从n个中取m个排列的个数
$$
A_{n}^{m}=\frac{n!}{(n-m)!}
$$
实际计算中,往往不用阶乘。从大的数字开始往小乘,乘“小的数字那么多”个
去重
例:1.2.3.4.5有5!种排序方式,而1.1.3.4.5的排序方式有5!/2!种:
“5!”意味着将1.1.3.4.5视作5个不同的元素,而这与实际不符,若两个“1”是不同的,交换后是2种序;但它们相同啊,所以“5!”计算出的结果,是将实际情况重复计算了2次,那么除以2就是正确答案了。
同理:
1.1.2.3.4.4.4.5可组成多少个8位数?答:8! / (2! x 3!)
组合公式
Combination 组合
组合不需要考虑排序
从n个中取m个组合的个数
$$
C_n^m=\frac{n!}{(n-m)!m!}
$$
实际计算中,往往不用阶乘。从大的数字开始往小乘,乘“小的数字那么多”个,再除以“小的数字开始往小乘,乘小的数字那么多个”。
排列与组合的关系
$$
C_n^m=\frac{\mathrm{A}_n^m}{\mathrm{A}_m^m}=\frac{n(n-1)(n-2)\cdots(n-m+1)}{m!}=\frac{n!}{m!(n-m)!}
$$
动态规划
动态规划是运筹学的一个分支,求解决策过程最优值的一种思想
求解最优解的时候需要想到动态规划
本质就是:给定一个大问题,把它拆成一个个子问题,直到子问题可以直接解决.然后把子问题的答案保存起来,以减少重复计算.再根据子问题答案反推,得到大问题解题的一种方法
动态规划中最重要的两个概念
- 重叠子问题
- 最优子结构
重叠子问题:动态规划会将每个求解过的子问题的解记录下来,这样当下一次碰到同样的子问题时,就可以直接使用之前记录的结果,而不是重复计算。(虽然动态规划使用这种方式来提高计算效率,但不能说这种做法就是动态规划的核心)
如果一个问题可以被分解成若干个子问题,且这些子问题会重复出现,那么称这个问题拥有 重叠子问题(Overlapping Subproblems)。
如果一个问题的最优解可以由其子问题的最优解有效地构造出来,那么称这个问题拥有 最优子结构(Optimal Substructure)。最优子结构保证了动态规划中原问题的最优解可以由子问题的最优解推导而来
一个问题必须拥有重叠子问题和最优子结构,才能使用动态规划去解决
动态规划通过额外空间避免重复计算来加速计算过程,由于用到其余空间来保存计算结果,因此也称之为记忆化搜索(Recursion with Memoization),本质上是用空间换时间,也有人叫他”带备忘录的递归”,或者递归树的剪枝(pruning).因为整个递归树不需要全部访问到,仿佛有些枝叶被剪掉了.上面说的递归也可以是迭代,动态规划不一定得是递归
动态规划的两种写法:
- 递推写法:自底向上(Bottom-up Approach),即从边界开始,不断向上解决问题,直到解决了目标问题;
- 递归写法:自顶向下(Top-down Approach),即从目标问题开始,将它分解成子问题的组合,直到分解至边界为至。
标准的动态规划实例:爬楼梯问题
动态规划与其他思想的差异
分治算法与动态规划——重叠子问题
- 相同点:
将问题分解成子问题,然后合并子问题的解得到原问题的解。 - 不同点:
分治法解决的问题不拥有重叠子问题,解决的问题不一定是最优化问题;
动态规划解决的问题拥有重叠子问题,解决的问题一定是最优化问题。
贪心算法与动态规划——最优子结构
- 相同点
都要求原问题必须拥有最优子结构。 - 不同点
贪心的计算方式类似于”自顶向下“,但是并不等待所有子问题求解完毕后再选择使用哪一个,而是通过一种策略直接选择一个子问题去求解,没被选择的子问题就不会再去求解了。
动态规划的计算方式有”自顶向下“和”自底向上“两种,都是从边界开始向上得到目标问题的解。也就是说,它总是会考虑所有子问题,并选择继承能得到最优结果的那个,对暂时没有被继承的子问题,由于重叠子问题的存在,后期可能会再次考虑它们,因此还有机会成为全局最优的一部分,不需要放弃。
53. 最大子数组和这题同时有贪心算法解法和动态规划解法(官方解释中有视频两种方式的视频讲解)
思路:
- 贪心算法:若当前指针所指元素之前的和小于0,则丢弃当前元素之前的数列.维护两个值:当前和,之前和
- 动态规划:若前一个元素大于0,则将其加到当前元素上.这样实际上存储的就是一个不确定左边界到当前边界的最大和,时间复杂度不如贪心算法
以赌场的骰子算法为例
问题就是: 通过Dice个骰子掷出总数为Total有多少种方式
递归回溯地思考问题,通过将大问题分解为相似的小问题来解决
以两个骰子为例,掷出一个总点数为8的话,第二次掷出的点数必须为1,2,3,4,5或6,所以要使总数为8,第一次掷骰必须分别为7,6,5,4,3或2,7是不可能的,用一个骰子掷出点数为6,5,4,3,2的方式都只有一种,因此,使用2个骰子掷出8个点数的方式是5种
准确地描述一个简单问题的解法能帮助我们找到更一般性的解决方案
可以总结为: 对于用n个骰子掷出m点的总数,那么前n-1个骰子必须掷出m-1,m-2,m-3,m-4,m-5或m-6的总数
这样就提供了一种递归算法,用来解决该问题
假设想用10个骰子掷出28的总和,那么前9个骰子的总和必须是27,26,25,24,23或22的一个,将一个问题拆解为多个问题,分别是用9个骰子掷出27 ,26,25,24,23,22这6个小问题
到这一步,就完成了递归式的遍历,但是如果仔细观察中间的步骤,就会发现有很多重复性的计算,因此可以采用类似缓存机制的方式来剪枝,于是就能大幅提高效率
这就是动态规划的原理: 通过递归的描述问题,即使用较小版本的相同问题来定义问题,再结合查找表保存我们已经完成的计算结果,我们通常可以显著加速这些算法
增益校正算法
路径规划算法
Dijkstra算法
Dijkstra算法迎来新突破:经典本科算法被证为普遍最优,最坏性能也达极限!
校验算法
CRC校验算法
CRC(循环冗余校验)算法可以提供更强大的校验功能,用于检测数据传输中的错误。CRC算法通过对数据进行多项式除法运算,生成一个固定长度的校验码(CRC校验码),用于校验数据在传输过程中是否发生了错误或被篡改。
CRC算法相比简单的校验和方法,具有以下优点:
- 更强的错误检测能力:CRC算法可以检测更多类型的错误,包括单比特错误、多比特错误、以及一些特定的错误模式。
- 低错误漏检率:CRC算法的设计可以降低错误漏检率,提高数据传输的可靠性。
- 固定长度的校验码:CRC算法生成的校验码长度固定,不受数据长度影响,便于在数据传输中使用。
在通信协议、存储系统、网络通信等领域,CRC算法被广泛应用于数据完整性校验。通过计算接收数据的CRC校验码并与发送数据的CRC校验码进行比较,接收方可以判断数据是否在传输过程中发生了错误,从而保证数据的可靠传输。
[计组#CRC循环冗余校验码|更多理解可以参考计组]
CRC16
以CRC16为例
1 | using System; |
也有查表法
基于c#的实现
1 | // |
基于C/C++实现
1 | static unsigned char auchCRCHi[] = { |
校验和计算
数据分割:将待发送的数据按照固定的单位(如字节)进行分割,每个单位称为一个数据块。
加和计算:对每个数据块中的值进行加和运算,生成一个校验和值。通常采用模2加法(二进制异或运算)或者累加和的方式进行计算。
模2加法的特点包括:
- 与传统加法不同,模2加法中进位被忽略,只关注每个位上的值。
- 模2加法满足交换律和结合律。
- 任何数与0进行模2加法得到原数。
- 任何数与自身进行模2加法得到0。
校验和附加:将计算得到的校验和值附加到数据中,一起发送给接收方。
接收端校验:接收方在接收数据后,对接收到的数据进行相同的加和计算,得到一个校验和值。
比较校验和:接收方将计算得到的校验和值与接收到的校验和值进行比较。如果两者相等,则数据传输过程中没有出现错误;如果不相等,则表示数据可能存在错误,需要进行相应的处理(如重新发送数据)。
1 | private byte CalCheckSum(byte[] command) |
校验和是一种简单有效的数据完整性校验方法,适用于对数据传输中的随机错误进行检测。然而,校验和并不能提供纠错能力,只能检测错误并提示出错的可能性。在需要更强大的错误检测和纠正能力时,通常会采用更复杂的校验算法,如CRC(循环冗余校验)等。
令人惊叹的平方根算法
平方根快速计算算法
另外,还有一种被称为“神奇的方法”的算法,它使用了一个特殊的常数和牛顿迭代法来快速计算平方根。
闭环控制算法
专业术语
测量值(PV,Process Variable)
这是控制系统中的一个术语,指的是控制过程中实际测量到的值,比如温度、压力、流量等过程变量的实时测量值。
在温度控制系统中,PV通常指的是当前的温度读数。
PV是控制系统的反馈部分,控制系统会根据PV与设定值(SV)之间的偏差来调整输出,以保持过程的稳定。
设定值(SV,Set Variable) 是用户设定的目标值,即希望控制系统达到的值。
操作输出值/控制输出值(MV,Manipulated Variable):是控制器输出的控制信号,用于驱动执行器(如阀门、电机等),从而影响PV。是控制器用来调整PV的控制动作的量级。
MV是控制器用来影响PV的输出信号,而PV向SV靠近的过程是控制系统响应MV变化的结果。MV的大小和方向取决于控制器如何解释PV与SV之间的偏差。如果PV低于SV,控制器可能会增加MV来增加输出(例如打开阀门或增加加热),如果PV高于SV,控制器可能会减少MV来减少输出(例如关闭阀门或减少加热)。
PID控制算法
PID控制是一种线性控制,它将给定值(t)与实际输出值y(t)的偏差的比例(P),积分(I),微分(D)通过线性组合形成控制量,对被控对象进行控制。
控制系统通常根据有没有反馈会分为开环系统和闭环系统,在闭环系统的控制中,PID算法非常强大
工业应用上占了95%的应用比例,使用起来简单,无需精确建模
其三个部分分别为
- Proportion 比例 比例组件根据过程距设定点的距离按比例施加作用力
- integration 积分 积分组件会努力将过程返回到设定点,误差存在的时间越长,量越大,积分输出越大
- differential 微分 微分组件着眼于过程远离设定点的速度,相当于预测未来的误差来调整输出
PID适用于二阶以内的线性系统 (线性指满足齐次性和叠加性,2阶以内是指系统动态方程中导数的最高次数在2以内)
针对高阶系统 可以化为 二阶系统
针对非线性系统 可以通过 李雅普诺夫线性化 近似为线性系统

PID算法可以自动对控制系统进行准确且迅速的校正,因此被广泛地应用于工业控制系统 参考
PID公式
下面过程出自此博客
PID控制的完整公式实际上是:(e是误差)
$$
C=\frac{1}{P}(e+\frac{1}{T_{i}}\int_{0}^{t}e{dt}+T_{d}\frac{de}{dt})
$$
实际上常用的是:
$$
C=k_{p}e+k_{i}\int_{0}^{t}edt+k_{d}\frac{de}{dt}
$$
离散化后如下:
$$
\begin{aligned}&\text{比例项: }K_pe(t)\xrightarrow{\textbf{离散化}} K _ p e _ k \\text{ 积分项: }&K_i\int_0^{t_k}e(\tau)d\tau\xrightarrow{\text{离散化}} K _ i \sum _ { i = 1 }^{k}e(i)\Delta t\&\text{微分项: }K_d\frac{de(t_k)}{dt}\xrightarrow{\text{离散化}} K _ d \frac { e ( k ) - e ( k - 1 ) }{ \Delta t}\end{aligned}
$$
分别看
比例项 $K_pe_k$
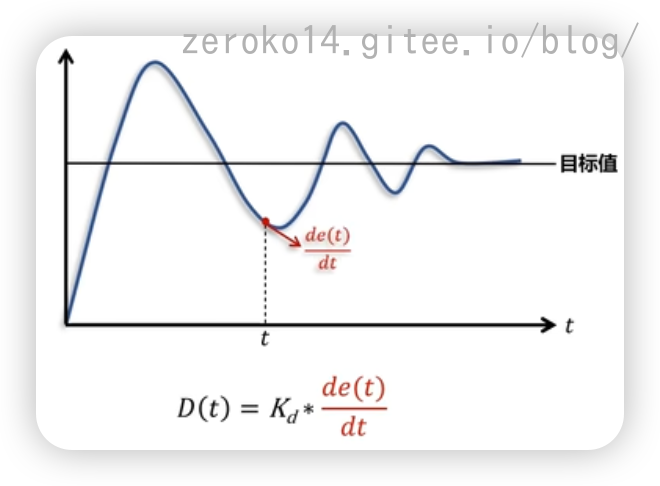
$e_k$表示x点的状态值与目标状态值的偏差(如图$e_x$就是$e_k$)
积分项 $K_i\sum_{i=1}^ke(i)\Delta t$
$\sum_{i=1}^ke(i)\Delta t$表示为下图三个颜色块的面积之和
微分项 $K_d\frac{e(k)-e(k-1)}{\Delta t}$
$\frac{e(k)-e(k-1)}{\Delta t}$表示下图中点的微分
离散化后得到PID的离散表达式:
$$
u(k)=K_pe_k+K_i\sum_{i=1}^ke(i)\Delta t+K_d\frac{e(k)-e(k-1)}{\Delta t}
$$
由于$\Delta t$是固定值,将$\Delta t$归入K中就得到了位置式PID

根据$\Delta u(k)=u(k)-u(k-1)$可得到增量式PID的离散公式如下:
$$
\Delta u(k)=K_p(e(k)-e(k-1))+K_ie(k)+K_d\left(e(k)-2e(k-1)+e(k-2)\right)
$$
- $k_{p}$ 比例增益:决定减少误差的速度的参数
- $k_{i}$ 积分增益:取决于之前所有误差的累积.消除了稳态误差,但也可能引入震荡
- $k_{d}$ 微分增益:取决于误差变化速度.增加阻尼减弱震荡效果增加稳定性:当偏差变化过快,微分环节会输出较大的负数,作为抑制输出继续上升,从而抑制过冲。
位置式PID和增量式PID本质是同一个公式
在真正使用PID控制算法的时候:最好还要做到:积分限幅,积分分离,微分先行
PID代码
pid.h
1 |
|
pid.cpp
1 |
|
测试代码
1 | PID pid2 = PID(0.1, 100, -100, 0.1, 0.01, 0.5); |
现成的pid算法
- Boost库里有PID控制器的封装。Boost::PID是基于boost::ublas的PID算法实现,提供基本的PID功能。
- Arduino库内的PID.h头文件封装了PID控制器类,支持增量式PID算法。
- OpenCV库中的cv::PIDController类实现了离散PID控制器。
- GNU科学库GSL中的gsl_control_pid_ss函数提供了单点离散PID控制。
- Eigen库中有BasicPIDControllers类实现基本PID控制。
PID变种
PI 控制器:
仅使用比例和积分控制,适用于对稳态误差要求较高的系统,但不需要微分控制。
PD 控制器:
仅使用比例和微分控制,适用于快速响应的系统,能够减少超调,但不能消除稳态误差。
PID 控制器:
经典的 PID 控制器,结合了比例、积分和微分控制,适用于大多数工业控制系统。
自整定 PID 控制器(Auto-tuning PID):
具有自动调节参数的功能,可以根据系统的响应自动调整 Kp、Ki 和 Kd 的值。
模糊 PID 控制器:
将模糊逻辑与 PID 控制相结合,通过模糊规则来调整 PID 参数,以适应非线性系统。
滑模控制(Sliding Mode Control):
在控制过程中引入滑模控制策略,以提高系统的鲁棒性和抗干扰能力。
增益调度 PID 控制器:
根据系统状态或工作点动态调整 PID 参数,适用于具有非线性特性的系统。
复合 PID 控制器(Cascade PID):
将多个 PID 控制器级联在一起,形成复合控制策略,以提高控制性能。
位置 PID 控制器与速度 PID 控制器:
针对不同的控制需求,分别设计用于位置控制和速度控制的 PID 控制器。
抗饱和 PID 控制器:
在积分部分引入抗饱和机制,以防止积分风up现象,确保系统稳定性。
PID 控制器的变种(如 PIDF、PI-D、PD-I):
这些变种根据具体需求,调整了 PID 控制器的组成部分,例如引入前馈控制、调整积分和微分的计算方式等。
PID参数评估
时域指标(动态响应)
- 超调量(Overshoot, $M_p$):响应曲线超过设定值的最大偏差百分比。优秀PID参数应使超调量<10%(高精度场景要求<5%)。
- 上升时间($t_r$):响应从稳态值10%升至90%所需时间。需平衡速度与超调,过快易引发振荡。
- 调节时间($t_s$):系统进入并保持在设定值±5%误差带内的时间。代表收敛速度,典型要求为<系统主时间常数。
- 稳态误差(Steady-state Error):系统稳定后与设定值的偏差。积分项(I)可消除稳态误差,但过度会导致超调。单位就是检测的值本身的单位
- 峰值时间($t_p$):达到第一个峰值所需时间,反映初始响应速度。
这些性能指标(超调量、上升时间、调节时间、稳态误差和峰值时间)的计算只需要两个核心数据:
- 设定值(Setpoint,SP):控制系统期望达到的目标值
- 过程变量(Process Variable,PV):被控对象实际反馈的测量值
频域指标(鲁棒性)
相位裕度(PM):开环传递函数在增益交界频率处的相位偏移量。PM>45°表明系统稳定。
增益裕度(GM):系统达到临界稳定前可增加的增益倍数。GM>6dB为安全边界。
带宽(Bandwidth):系统有效跟踪输入信号的频率范围,带宽越宽响应越快,但噪声敏感性增加。
阶跃响应法
ZN整定法
临界震荡法
Lambda整定
PID调参参考
参考指标: SP(设定点)曲线 ,PV(过程变量)曲线,OUT(控制输出)曲线, 积分项(Integral_Sum)曲线
- 初始准备
- 设置初始限幅 初始按照物理限制设置输出限幅区间,初始积分限幅为(最大值-最小值)*0.2左右
- PID初始值: P=0,I=0,D=0
- 调节P值
- 从纯P (
I=0, D=0)开始,小步增加P,找到临界振荡点 (Ku(临界增益),Pu(临界周期)) - 初始工作点P:
P = Ku / 2.5或P = Ku / 3(倾向于更保守以缓解后续I和积分限幅的压力)
- 从纯P (
- 调节I值
- 保留上一步得到的
P,设定一个较小的I(例如I = P * 0.05或基于Pu如I = 0.6 * P / Pu) - 小步长提高I,观察目标,系统趋向稳定,查看积分项曲线,应该在积分限幅内活动,暂时不要撞到限幅
- 如果系统不稳定或震荡加剧: 减小I或略微减小P,目标是得到一个有稳态误差但过程平稳的响应
- 观察积分项的值是否达到了饱和(积分限幅)?
- 积分项没有饱和(仍在积分限幅内): 说明当前的I太小了,稍微增大I,重复这个过程直到积分项开始接近积分饱和,或者稳态误差消失
- 积分项已经饱和,但仍然有显著的稳态误差: 说明消除此误差所需的积分贡献超出了你设定的积分限幅.此时保持I不变,仅小步幅增大积分限幅,直到稳态误差归零或小于要求精度
- 保留上一步得到的
- 调节D值
- 保持调好的P,I,积分限幅,加入小D
- 小步增大D,目标是抑制超调,加快系统响应
- 如果输出抖动,输出噪声放大,如果有则立即减小D,许多系统不需要D(特别是噪声大的系统)
- 整体微调
适用于非线性系统的控制算法
- 模糊控制(Fuzzy Control)
- 自适应控制(Adaptive Control)
- 滑膜控制(Sliding Mode Control)
- 非线性反馈控制(Nonlinear Feedback Control)
- 神经网络控制(Neural Network Control)
- 预测控制(Model Predictive Control, MPC)
- 增益调度(Gain Scheduling)
模糊控制算法
Fuzzy Logic Control(FLC)
模糊化是根据特定输入值的拟合程度,将特定输入值转换为模糊集某种程度的隶属度的过程
隶属函数描述特定输入或输出变量,这些隶属函数可以用图形表示

这些隶属函数有助于量化基于语言变量,而不是精确数值做出决策所涉及的模糊逻辑
模型预测控制
Model Predictive Control(MPC)
是一种反馈控制技术,基于数学模型预测系统未来行为的控制算法
作为许多工业应用中强大且广泛使用的控制策略
其他控制算法
- 自适应控制算法
- 神经网络控制算法
多因子PID控制
PID控制器可以实现多个控制因子对一个最终采样值的控制,称为多输入单输出(MISO)控制系统
三种主要实现方法
多变量并行PID控制
各控制因子独立影响输出,作用可线性叠加
用于PID的温度仿真模拟
1 | public class SimulationTemperature |
快速傅里叶变换算法
[[数学#傅里叶变化|参考傅里叶变换数学原理]]
基于fft的快速快速乘法
物理仿真算法
运动学算法
此处收录一个程序化动画技术视频链接,生物模拟,机械臂等都属于这个可用范围中
设置一个锚点,并通过[[数学#圆参数方程|圆参数方程]],约束下一个点的位置,如果移动锚点,下一个点也会跟随锚点移动
将多个点用这种约束串联起来,使每个点都能约束到下一个点.当我们移动第一个点的时候,整个链条会按照我们的约束的顺序跟随移动

然后如果有需要可以添加每两节体节的角度平滑:给定任意两体节,若干角度差太大,缩回至所需阈值
正向运动学
Forward Kinematics
通过多个向量相加计算出目标的坐标点
反向运动学
Inverse Kinematics
由目标坐标点,如何找到正确角度旋转手臂
有一种非常简单的近似技术,FABRIK
碰撞检测
最简单的思路就是遍历所有两个对象之间的重叠判断,以圆为例就是判断两个对象锚点间的距离小于两半斤之和则为重叠
这样可以做到碰撞检测,但是效率十分低下,低效之处在于两个远离的对象之间执行了很多无用的检查
因此必须引入空间分割的概念
最简单的结构之一就是固定网格加速
FABRIK
FABRIK(Forward and Backward Reaching Inverse Kinematics)是一种用于逆向运动学(Inverse Kinematics, IK)求解的算法,广泛应用于计算机动画、游戏开发和机器人运动控制等领域。它的主要目的是通过调整关节的位置来实现目标位置的达成,通常用于角色动画和机械臂控制。
在锚点和目标点之间不断重复来回拉扯机械臂,直到收敛于从锚点开始并朝向目标位置的排列
FABRIK基本原理
FABRIK 算法的核心思想是通过前向和后向的迭代过程来求解关节的位置,使得末端效应器(如手、脚等)能够达到目标位置。具体步骤如下:
- 初始化:设置关节的初始位置和目标位置。
- 前向迭代:
- 从根关节开始,逐个更新关节的位置,使得每个关节与其下一个关节之间的距离保持不变。
- 这一过程会将末端效应器逐渐移动到目标位置。
- 后向迭代:
- 从末端效应器开始,逐个更新关节的位置,使得每个关节与其上一个关节之间的距离保持不变。
- 这一过程会确保关节的运动不会超出其物理限制。
- 重复迭代:重复前向和后向迭代,直到末端效应器接近目标位置或达到预设的迭代次数。
LQR控制器
工业上的平滑算法
在工业上,当传感器测得的数据波动非常大时,常用的方法之一是数据平滑处理。以下是几种常见的数据平滑方法:
- 移动平均法:计算一定时间窗口内的数据平均值,用平均值替代原始数据点。移动平均法可以有效地减少数据的波动,使数据更加平滑。
- 指数加权移动平均法:与简单移动平均法不同,指数加权移动平均法给予最近数据点更大的权重,使得平均值更加灵活地跟随数据的变化。
- 滤波器:使用数字滤波器对数据进行滤波处理,常见的滤波器包括低通滤波器和中值滤波器(滑动窗口取排序后的中位数),小值滤波器(滑动窗口取排序后的最小值)等。滤波器可以有效地去除数据中的噪声和波动。
- 数据插值:通过插值算法对数据进行插值处理,填补数据中的缺失或异常值,使得数据更加平滑。
现在是这个这样的情况,我需要实时修正一组数据的离群点,数据点以一秒一个的方式获取到,需要实时处理已经出现的数据点中的异常点,这些离群点可能连续几个上下连续大幅以激变的形式出现,我需要将这样的异常点找出来.并且不具备任何的数学模型,是否有合适的算法可以使用
卡拉楚巴算法
属于底层数学原理,上层用不上
优化乘法运算的复杂度
滤波器
- 消除噪声:平均滤波器、高斯滤波器、维纳滤波器
- 保留边缘细节:中值滤波器、高斯滤波器
- 动态系统状态估计:卡尔曼滤波器、自适应滤波器
- 图像处理:高斯滤波器、卷积滤波器
- 音频处理:巴特沃斯滤波器、切比雪夫滤波器
常用滤波器介绍
优势:
- 对于脉冲噪声(如盐椒噪声)效果显著,能有效去除异常值。
- 保留边缘细节,不会模糊图像。
适用场景:
- 图像处理中去除单像素噪声。
- 传感器数据处理,去除瞬时噪声。
平均滤波器 (Mean Filter)
优势:
- 简单易实现,计算速度快。
- 平滑效果较好,能有效消除高频噪声。
适用场景:
- 需要快速处理的信号平滑。
- 对频谱不敏感,适合于一般噪声的平滑。
高斯滤波器 (Gaussian Filter)
优势:
- 保留图像细节,平滑效果较为自然。
- 通过调节参数可以控制平滑程度和边缘保留效果。
适用场景:
- 图像处理中常用的模糊滤波方法。
- 需要平滑信号但又不希望失去细节的情况。
优势:
- 频率响应平坦,截止频率处不产生波纹。
- 可以实现比较陡峭的频率特性。
适用场景:
- 通信系统中的滤波器设计。
- 需要平滑频率响应的应用,如音频和语音处理。
切比雪夫滤波器 (Chebyshev Filter)
优势:
- 可以实现非常陡峭的频率特性。
- 在通带或阻带允许一定纹波情况下,能提供更好的截止特性。
适用场景:
- 对频率响应要求较高的通信和雷达系统。
- 需要在频域上实现比较严格的要求。
维纳滤波器 (Wiener Filter)
优势:
- 根据信号和噪声的统计特性自适应调整滤波器参数。
- 在知道信号和噪声的统计特性时,能够达到最优的去噪效果。
适用场景:
- 信号和噪声的统计特性已知,如通信系统中的信号重建和去噪。
优势:
- 可以对动态系统的状态进行估计和预测,适用于非线性和线性系统。
- 通过状态预测和更新,能够提供最优的估计结果。
适用场景:
- 航空航天、导航系统中的位置和速度估计。
- 移动机器人的轨迹跟踪和状态估计。
自适应滤波器 (Adaptive Filter)
优势:
- 能够动态调整滤波器参数,根据信号特性自适应地优化滤波效果。
- 在信号特性随时间变化或环境变化的情况下,能够保持较好的滤波效果。
适用场景:
- 信号特性动态变化的自适应滤波需求,如通信、雷达和生物信号处理。
梯形滤波器 (Trapezoidal Filter)
优势:
- 通过加权平均当前和前后若干点的数据,能够较好地平滑信号。
- 权重的梯形分布有助于保留信号的边缘细节。
适用场景:
- 需要在平滑信号的同时保留边缘细节的应用,如图像和声音处理。
卷积滤波器 (Convolution Filter)
优势:
- 通过卷积运算处理信号,可以实现多种复杂的滤波效果。
- 在图像处理和深度学习中有广泛应用,能够实现多种空间和频域上的滤波需求。
适用场景:
- 图像处理中的边缘检测、模糊处理和特征提取。
- 深度学习中的卷积神经网络中的特征卷积。
中值滤波
中值滤波是一种常用的信号处理方法,用于去除噪声和平滑数据。它通过将每个点替换为其邻域窗口中的中值,从而有效地去除尖锐的噪声
边缘效应:对于数据集的边缘部分,由于窗口的一部分会超出数据边界,可以采用不同的策略处理边缘(如重复边缘数据、补零、仅使用有效数据等)
下面提供一个中值滤波的例子
1 | public static List<double> MedianFilter(List<double> data, int windowSize) |
一阶(αβ)滤波
一阶滤波是比较常用简单的滤波方法,就是当前采样结果和上一个滤波结果加权求和,权重和为1。对周期干扰噪声有良好的抑制作用,但同样会产生相位滞后,权重是固定值也是其缺点之一。
巴特沃斯滤波
巴特沃斯滤波器(Butterworth Filter)是一种数字滤波器,常用于信号处理领域中对频率进行滤波和调整。巴特沃斯滤波器的设计基于巴特沃斯多项式,具有平滑的频率响应曲线和良好的通频带特性。
巴特沃斯滤波器在信号处理中具有广泛的应用,可以帮助滤除噪声、调整信号频率特性、设计滤波器等
巴特沃斯滤波器主要用于解决以下问题:
- 信号滤波: 巴特沃斯滤波器可以对信号进行滤波,去除不需要的频率成分,保留感兴趣的频率成分。这在信号处理中常用于去除噪声、平滑数据、提取特定频率成分等。
- 频率调整: 巴特沃斯滤波器可以调整信号的频率特性,包括增强或抑制特定频率范围内的信号。这在音频处理、图像处理、通信系统等领域中很有用。
- 滤波器设计: 巴特沃斯滤波器是一种经典的滤波器类型,其设计方法相对简单且易于实现。因此,它常被用于滤波器设计中,满足不同应用场景的频率响应要求。
卡尔曼滤波
我的理解:一句话概括就是理论值和实际值的加权平均
卡尔曼滤波(Kalman Filtering)是一种用于估计系统状态的最优滤波算法。它基于对系统的动态模型和测量模型进行建模,通过递归地更新状态估计值,提供对系统状态的最优估计和预测。
卡尔曼滤波在以下情况需要使用
- 当系统受到噪声干扰时,需要准确估计系统的状态。
- 当系统具有复杂的动态模型或多个传感器测量值时,需要融合这些信息来得到更准确的状态估计。
- 当系统需要快速响应和准确跟踪目标时,卡尔曼滤波可以提供更优秀的性能。
- 当系统需要实时进行状态估计,并且需要考虑系统的动态特性和测量误差时,卡尔曼滤波是一个有效的选择。
这里我们就不扯那些专业术语了,我们讲“人话”。首先我们需要对卡尔曼滤波具体是干什么的要建立起一个最基本的概念,这里先借鉴知乎用户Kent Zeng的说法,给大家打一个大致的基础。
假设你现在处于某颗星球上,手上有两个力传感器,并且有一个已知质量为m的物体,但是你不清楚他们的重力大小,而且你也不知道你现在所处位置的重力加速度的具体值为多少,因此你打算通过两个传感器获得物体的重力。
但不幸的是它们测得的读数似乎每次都不太一样,那该怎么办?没错,就是取平均。
再假设你知道其中贵的那个传感器应该准一些,便宜的那个应该差一些。那有比取平均更好的办法吗?没错,加权平均。
再然后,假如你手上只有一个传感器,但是你碰巧得知了当地的重力加速度为g,那么你现在可以知道传感器测出的重力值为G1,你自己通过数学模型推导出来的重力G2 = mg,但是这两个值之间似乎也有偏差,那该怎么办呢?
没错,我们还是取两值的加权平均,但是你不清楚G1和G2哪个更加可信,那么如何确定权值系数?这取决于你对这个g值的确信度,如果你更相信数学模型mg的推导结果,那么对应数学模型的权值更大,而你传感器的观测模型的权值则变小;如果你对g的确信度较小,那么就正好相反。而这个权值,在卡尔曼滤波中也叫作卡尔曼系数。
以上,就是卡尔曼滤波最基本的思想。没错,是不是很简单呢?当然,在这之中我们也忽略掉了一些东西,但是不要着急,我们一步一步来。
卡尔曼滤波实际上就是把传感器测得的值和根据数学模型推导出来的值融合以逼近实际值的过程,因此卡尔曼滤波也经常被称作传感器融合算法。

左侧正态分布表示汽车起始点,经过一段时间后,右侧蓝色正态分布表示汽车计算出来可能落到的正态分布,右侧红色正态分布表示传感器测量出来的正态分布,卡尔曼滤波测出来的正态分布为右侧灰色正态分布
通过数学模型预测得到了k时刻的位置估算值,然后将其与小车传感器的测量值进行结合,得到了当前k时刻小车的最佳位置估算值
卡尔曼滤波的思想:
- 卡尔曼滤波是利用线性状态模型,以及模型的输入和输出值,结合传感器测量值获取当前时刻的最佳状态估计值;
- 卡尔曼滤波假设所有的不确定性因素理论上都服从正态分布;
- 卡尔曼滤波就是使最后估算状态的高斯分布的期望值能够接近实际值,并且方差够小;
- 卡尔曼滤波工作于连续的系统,并通过迭代操作估算每一个时刻的最佳状态估计值。

Car dynamics是小车的真实模型,内部的方程我们是不清楚的,这里只是为了更好地示意真实噪声环境下传感器测量结果的不确定性,我们能得知并且运用的,只有输入量$u_k$ 和传感器测量值 $k y_ky$;而 Car model 则是我们实际运用的数学模型,我们可以从中得出状态估计量 $\hat{x}$,其中w和v是随机噪声
波函数坍缩算法
该算法的命名来源于量子力学
$$
量子系统在测量过程中,从多个可能状态,逐渐坍缩到一个确定状态的现象。 —–量子力学-波函数坍缩
$$
- 需要制定约束规则
- 每当完成一个位置的坍缩后,会逐一调整剩余位置的可选坍缩可能
- 坍缩完成后下一个坍缩位置选择
- 对于各种坍缩可能概率一致的情况,选坍缩数量最少的位置进行坍缩,因为可选坍缩数量越少,代表这个位置对地图后续走向越关键,因此处理的优先级更高;并且对最小的可能性数量的坍缩结果进行坍缩会提高整体效率
- 对于各种坍缩可能不一致的情况,引入熵的概念,选择熵(概念上表示最稳定的位置)最小的位置作为下一个坍缩目标
熵
$$
熵 = -\sum_{i=1}^Np_i\log_2p_i
$$
$p_i$为第i个坍缩可能的概率
回溯机制
在坍缩的过程中可能会出现某个位置的可选坍缩可能数为0的情况,因此无法进行坍缩,为了解决这种场景,波函数坍缩算法加入了回溯机制:
每当完成一次坍缩后,算法会记录所有位置的状态快照,并将快照保存到一个栈中
当面临无解的情况,就可以回溯到有解的状态来避免做出那个选择
总结
- 制定约束规则,并在坍缩过程中不断调整剩余未坍缩位置的可选瓦片
- 计算未坍缩位置的熵值,并选择熵值最小的位置作为下一个坍缩目标
- 每次坍缩后保存状态快照,并在遇到无解的情况时进行回溯
模拟退火算法
在众多好的算法中寻找最优的算法
鸟群模拟算法
BOIDS算法是一种用于模拟鸟群行为的计算模型,由Craig Reynolds在1986年提出。该算法通过简单的规则来模拟个体(如鸟)之间的互动,从而形成复杂的群体行为。BOIDS模型主要基于三个基本规则:
- 分离(Separation):个体会避免与邻近的其他个体过于接近,以防止碰撞。
- 对齐(Alignment):个体会调整自己的运动方向,朝向鸟群的平均方向。
- 聚合(Cohesion):个体会朝向邻近个体的中心位置移动,以保持群体的整体性。
通过这三条简单的规则,BOIDS算法能够生成自然的群体运动效果,广泛应用于计算机图形学、动画、机器人技术等领域。
仅凭三条简单规则就能产生涌现复杂性或美丽
避障算法
插值算法
关于插值的详解:
线性插值
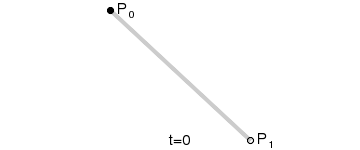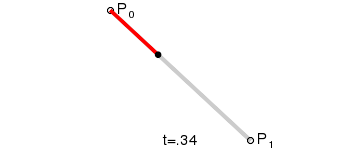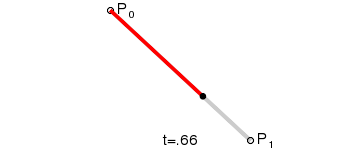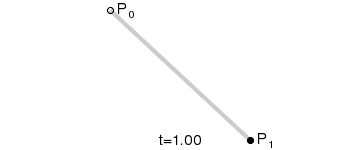
最简单的线性插值公式
 $$
对于0和1之间的任意t值,可以计算它们之间的百分比:A+(B-A)t
$$
线性插值最简单的公式就是👆🏻这样
$$
对于0和1之间的任意t值,可以计算它们之间的百分比:A+(B-A)t
$$
线性插值最简单的公式就是👆🏻这样
线性插值如下:
$$
\operatorname{lerp}(a, b, t)=(1-t) a+t b
$$
但是最后一个参数t可以玩出很多花样来:
$$
A+(B-A)f(t)
$$
1 | float lerp(float A,float B,t) |
$f(t)=t$的时候,这就是一个线性插值
于是一个插值函数可以概括为lerp(A,B,f(t))

上图绿线为$f(t)=t$,紫线为$f(t)=t*t$,此时就不是线性插值了,可以理解为插值的密度或权重变化了.如果把y轴理解成一个小球向上运动的小球,此时两个函数虽然他们还是在同一个点开始,同一个点结束,但是小球向上运动的速度却在变化,后者需要一个启动时间,就相当于被设置另一个固定的加速度,然后从0开始加速

同样,上图可见紫色线为$f(t)=sqrt(t)$,初始高速度弹射起步,固定的加速度降低速度
同样也有平滑曲线(从左到中间缓慢加速,中间到终点时缓慢减速,起点和终点附近曲线平缓,中间曲线最陡)可以通过上面两个函数得到:

下面盘点记录一下常用的函数
图1: 二次缓出 图2:二次缓入 图3:parabola 图4:Triangle三角形来回弹跳 图5:Elastic Out弹射起步,会超终点 图6:Bounce Out重力落地方式到终点,弹跳停止到终点 图7:缓入缓出,混合得到smoothstep函数
1 | //二次缓出 |
应用场景如
GPU采样纹理时,采用的双线性插值
界面元素采用Bounce函数等动画中利用这些变化
缩放的时候,使用
lerp(log(Z0),log(Z1),time)比使用lerp(Z0,Z1,time)更好对颜色进行插值很容易,比方说对蓝色到黄色进行插值,要用线性颜色空间进行插值,最后再转换回RGB空间,得到的渐变效果会更好
线性颜色空间是指在颜色表示中,颜色的数值与人眼对光强度的感知之间是线性关系的颜色空间。在这个空间中,颜色的数值(如 RGB 值)直接对应于物理光强度,这意味着如果一个颜色的数值是另一个颜色的两倍,那么它在视觉上看起来也会是前者的两倍亮度
阻尼
1 | //帧数无关的current向target的追踪效果,target是可以变化的 |
样条插值
用途:
- 根据数据做预测,或则根据局部情况估计整体分布
- 图形化呈现计算结果
缺点:不能给出明确函数关系,一般用于对数据的概括性描述,从中发现分布特征
样条名词解析:
“样条”这个术语源自于造船业,用来描述在木船的曲线形状中使用的一种柔软且易弯曲的木条。在数学和计算机科学领域,”样条”被引入用来描述一种平滑且连续的插值函数。因此,”样条插值”指的是通过连接相邻数据点的一系列曲线段来逼近数据的插值方法,以实现平滑的曲线拟合。 在样条插值中,通常会使用多项式函数来拟合相邻数据点之间的曲线段,以确保在数据点处函数值的连续性和平滑性。样条插值方法在数据处理、图像处理和数值分析等领域广泛应用,可以有效地处理数据的平滑和插值问题。
不用给出具体的函数关系,根据已有数据预测其他数据即可的情况可以使用样条插值算法
根据实际应用对于“平滑”的要求,通常会有以下不同的约束:
- 要求生成的参考曲线是连续的;
- 在1的基础上,要求参考曲线的速度是连续的;
- 在1和2的基础上,要参考曲线的加速度是连续的;
速度是位置对时间的导数,加速度是速度对时间的导数,加速度对时间的导数我们称之为jerk。
在多项式插值里面,给定多项式的阶次越高,能拟合的函数曲线就越复杂,但越高阶次的多项式对于计算资源的要求越多。因此对于这3个要求,我们可以分别用不同阶次的多项式函数来拟合,实际应用时根据需求选择合适的方法。
下面的公式讲解如下:$a_0$,$a_1$是待确定的常量参数。$t_0$表示初始时刻, $a_0$表示初始时刻的位置, $a_1$表示斜率,也就是速度,这里为常量。因此,给定下一个时刻 $t_1$处的位置 q($t_1$), $t_f$表示分割点时间
线性插值(一阶,恒定速度)
线性插值,顾名思义,就是使用线性的方法来进行插值。即将给定的数据点依次用线段连起来,点与点之间运动的速度是恒定值。
$$
q(t)=a_0+a_1(t-t_0)
$$
得出常数为:
$$
\left{\begin{array}{l}a_0=q_0\a_1=(q_1-q_0)/(t_1-t_0)\end{array}\right.
$$以C#代码为例,给出线性插值的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51private static double[] Interpolate(List<double> source, int targetLength)
{
double[] result = new double[targetLength];
double step = (double)(source.Count - 1) / (targetLength - 1);
for (int i = 0; i < targetLength; i++)
{
//result序列中第i个点对应的source原始序列中的下标:index
double index = i * step;
//整数部分
int indexInt = (int)index;
//小数部分
double frac = index - indexInt;
if (indexInt + 1 < source.Count)
{
//线性插值的关键体现
//result[i] 是在 indexInt 和 indexInt + 1 之间进行线性插值计算的值
// frac = 0时,目标位置在indexInt。
result[i] = source[indexInt] * (1 - frac) + source[indexInt + 1] * frac;
}
else
{
// 如果 indexInt 已经是最后一个索引,直接取其值
result[i] = source[indexInt];
}
}
return result;
}
//针对二维点的线性插值
/// <summary>
/// 生成指定个数的线性插值点
/// </summary>
/// <returns>插值点的列表</returns>
public static List<ObservablePoint> GenerateLinearInterpolationPoints(double x0, double y0, double x1, double y1, int numberOfPoints)
{
if (x1 == x0)
throw new ArgumentException("x0 和 x1 不能相同。");
List<ObservablePoint> points = new List<ObservablePoint>();
double step = (x1 - x0) / (numberOfPoints + 1);
for (int i = 1; i <= numberOfPoints; i++)
{
double x = x0 + i * step;
double y = y0 + (y1 - y0) * (x - x0) / (x1 - x0);
points.Add(new ObservablePoint(x, y));
}
return points;
}权重来看(这两边权重很容易理解反!)
- 左侧整数位置的权重:
1 - frac(越靠近左侧位置,权重越大) - 右侧整数位置的权重:
frac(越靠近右侧位置,权重越大)
- 左侧整数位置的权重:
抛物线插值(二阶,恒定加速度)
抛物线差值(Parabolic Spline)是二阶多项式插值方法。与线性插值法将各个数据点用线段连起来不同,抛物线插值方法是用二次曲线将各个数据点连接起来,在连接处使用平滑的曲线来过渡,而避免速度不连续导致的“急剧拐弯”。抛物线差值的特征是具有恒定的加速度/减速度,一般是由两个二阶多项式的组合来得到。为什么是两个二阶多项式呢?因为一个用于“加速阶段”,一个用于“减速阶段”。“加速阶段”和“减速阶段”的分割点叫flex point。
加速阶段
$$
q_a(t)=a_0+a_1(t-t_0)+a_2(t-t_0)^2,\quad t\in[t_0,t_f]
$$减速阶段
$$
q_b(t)=a_3+a_4\left(t-t_f\right)+a_5\left(t-t_f\right)^2\quad t\in[t_f,t_1]
$$
常数公式略
三次多项式插值(三阶,加速度可变)
三次多项式插值方法(Cubic Spline)是一种常用的插值方法,其位置和速度曲线是连续的,加速度是可变的,但加速度不一定连续。考虑2个数据点之间插值的情况,其数学表达式为:
$$
q(t)=a_0+a_1\left(t-t_0\right)+a_2(t-t_0)^2+a_3(t-t_0)^3,\quad t_0\leq t\leq t_1
$$
两种计算情况给定了初始时刻$t_0$和最终时刻$t_1$处的位置与速度信息($q_0,q_1,v_0,v_1$),设$h=q_1-q_0,T=t_1-t_0$,则参数可以使用一下公式计算:
$$
\left.\left{\begin{array}{l}a_0=q_0\a_1=\mathrm{v}_0\a_2=\frac{3h-(2\mathrm{v}_0+\mathrm{v}_1)T}{T^2}\a_3=\frac{-2h+(\mathrm{v}_0+\mathrm{v}_1)T}{T^3}.\end{array}\right.\right.
$$
对于给定 n 个一系列数据点进行插值的情况,只需要对所有相邻的两个数据点使用上述公式即可依次计算得到整条插值曲线。给定了每一个点的位置信息$(\begin{array}{c}q_0,q_1,\ldots,q_n\end{array})$,但中间点的速度未给定
这种情况,整条曲线最开始的起点和最终的终点速度需要直接给定,一般为零,$v_0=v_1=0$.中间各个数据点的速度可以通过启发式方法得到,即通过求解位置对时间的导数得到,那么对于第k个中间点,我们有:
$$
\left.v_k=\left{\begin{array}{ll}0,\quad sign(d_k)\neq sign(d_{k+1})\\frac12(d_k+d_{k+1}),\quad sign(d_k)=sign(d_{k+1})\end{array}\right.\right.
$$
其中$d_k=(q_k-q_{k-1})/(t_k-t_{k-1})$,表示曲线的导数或斜率,sign()为符号函数,返回1或-1直观理解:考察第k个数据点,若其导数在该点进行了符号反转,则该点速度为0,否则该点速度为其导数
可以看到,位置曲线是“平滑”的,速度曲线是连续的,加速度曲线是可变的,但是不连续。这样,对于高速控制的场合来说,控制器的输入仍然会存在阶跃,导致不连续的情况。
五次多项式插值(五阶,加速度连续)
略,更多详情参考此处
可以看出,位置、速度、加速度三条曲线都是连续的,并且位置和速度还是“平滑”的,如果加速度曲线也要求是平滑的,那么就需要更高阶次的多项式插值方法了,例如七阶多项式插值。
七次及更高阶次的多项式插值
各种方法插值的对比图

n次拉格朗日插值多项式: 太复杂,但能推出一个统一的多项式
分段线性插值: 针对每两个点,分段进行线性插值
三次样条插值的Matlab语法
1 | #matlab语法 |
分段三次多项式插值

拉格朗日算法
贝塞尔曲线
线性插值如下:
$$
\operatorname{lerp}(a, b, t)=(1-t) a+t b
$$
用于描述一个点在两点之间的移动轨迹,实际上就是个线性插值算法
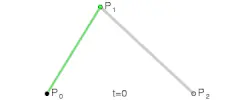
二阶贝塞尔曲线
这里的 P0、P1、P2 分别称之为控制点,贝塞尔曲线的产生完全与这三个点位置相关。
三个匀速前进的点(各自速度不同),分别是沿着P0到P1,P1到P2,以及沿着绿色线前进,同时从起点出发,同时到达终点
三阶贝塞尔曲线
四阶贝塞尔曲线
贝塞尔曲线可以由阶数递归定义
这也就意味着,我们可以通过调节控制点的位置,进而调整整个曲线。
公式

通过递归地应用lerp函数可以实现任意阶数的贝塞尔曲线
1 | public struct Point |
Lerp 方法:
这个方法通过两个点和一个参数 t 来计算它们之间的线性插值。
RecursiveBézier 方法:
这个方法会逐步对相邻的控制点进行插值,直到只剩下一个点。对于每个递归调用,我们会生成一个新的控制点列表,其中每个新的控制点都是相邻原始点之间的线性插值。
GenerateBézierCurve 方法:
这个方法遍历 t 的值(从 0 到 1),并调用 RecursiveBézier 来生成贝塞尔曲线上的点。通过调整 step 的大小,你可以控制贝塞尔曲线的精度。
还有公式实现法,效率更高,公式推导参考
使用公式实现的算法,暂略
分段贝塞尔曲线
虽然贝塞尔曲线的阶数可以很高,但是如果曲线的阶数过高,调整控制点对曲线的影响就比较小,调整起来相当麻烦。因此常常使用分段的贝塞尔曲线来保证每一小段不会太复杂
分段带来的唯一问题是,曲线在段与段的交界处,如何保证平滑?
所谓平滑,其实就是一阶导数连续(导数的值不会出现突变(跳跃)或不连续的情况),也就是左右导数的极限相同。
对两侧的贝塞尔曲线求导,分别代入 t=0 和 t=1 (即贝塞尔曲线的开始和结束时间),让二者相等。此时能发现,当两侧控制点与分段交接点共线且形成的线段长度相等时,满足曲线平滑性质。

曲线相关算法
曲线平滑
样条插值算法就可以作为一种曲线平滑算法
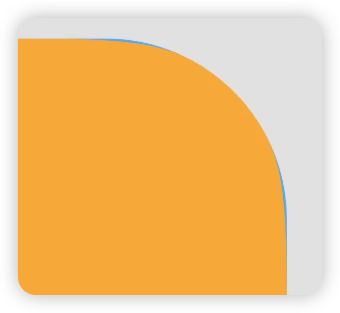
圆角平滑算法
圆的曲率为半径的倒数,直线的曲率为0
在二维空间中,曲线的曲率可以通过其切线的变化率来定义。具体来说,曲率 ( k ) 可以表示为:
$$
k = \frac{d\theta}{ds}
$$
其中 ( $\theta$ ) 是切线的角度,( $s$ ) 是沿着曲线的弧长。
在三维空间中,曲面的曲率通常用高斯曲率和平均曲率等来描述,这些曲率量化了曲面在不同方向上的弯曲程度。
在曲率的圆角设计中,G1、G2 和 G3 是用于描述曲线连接的几何连续性标准。这些标准通常用于 CAD(计算机辅助设计)和计算机图形学中,以确保曲线或曲面的平滑连接。具体来说:
G1 连接(一次连续性):
- G1 连接要求在连接的两个曲线或曲面之间具有相同的端点位置,并且在该点的切线方向相同。换句话说,G1 连接确保了曲线在连接点处是连续的,但可能会有角度的突变。这种连接适用于对平滑度要求不高的情况。
G2 连接(二次连续性):
- G2 连接不仅要求连接的曲线在端点位置相同,而且要求在连接点的切线方向(即一阶导数)也相同。这意味着在连接点处,曲线的斜率是连续的,从而提供了更高的平滑度。G2 连接适用于需要更高平滑度的设计。
G3 连接(三次连续性):
- G3 连接要求在连接点处,不仅切线方向相同(G2),而且切线的变化率(即二阶导数)也相同。这意味着在连接点处,曲线的加速度也是连续的,从而提供了最高级别的平滑度。G3 连接通常用于对光滑度要求极高的应用,比如高端工业设计和汽车外观设计。
G1,G2,G3对比:

G2的问题如下:

下图蓝底为G1平滑,黄色为G3平滑
苹果的圆角设计为G3圆角,是一种看起来更自然更舒服的圆角
超椭圆
小米的logo设计利用的是超椭圆公式,适合用于做logo底图
超椭圆公式:
$$
|x|^{n}+|y|^{n}=1
$$
超椭圆也称为拉梅曲线,
是在笛卡尔坐标系下满足以下方程式的点的集合。
- n=2时:该曲线就是圆的曲线
- n>2时:圆角矩形(小米logo的轮廓就是n为3时的超椭圆)

曲线相似算法
动态时间归整算法也可以作为曲线相似算法
Fréchet距离算法
弗雷歇距离(Fréchet Distance)是一种用于测量两条曲线或路径之间相似性的距离度量,由法国数学家Maurice René Fréchet在1906年提出的一种路径空间相似形描述(此外还在这篇论文里定义了 度量空间),这种描述同时还考虑进路径空间距离的因素,广泛应用于计算机科学、图形学、地理信息系统等领域。与传统的欧几里德距离不同,Fréchet距离不仅考虑曲线上的点对点距离,还考虑曲线的形状和走向。
Fréchet距离是一种强大的曲线相似性度量方法,通过考虑曲线的形状和走向,能够更精确地衡量两条曲线之间的相似性。在实际应用中,可以通过动态规划等方法来计算该距离,并结合修正值处理数值计算中的不精确性。尽管计算复杂度较高,但在需要精确比较曲线的场景中,Fréchet距离具有无可替代的重要性。
应用场景
计算机图形学:用于比较和对齐曲线、形状匹配。
地理信息系统:用于路径比较、轨迹相似性分析,如分析动物迁徙路径或车辆行驶轨迹。
模式识别和机器学习:用于时间序列分析、手写字符识别等。
优点
- 能够有效地比较曲线的形状和几何特征
- 考虑了曲线的连续性和走向,适合路径和轨迹比较
缺点
- 计算复杂度较高,特别是在处理高维数据时
- 动态规划方法在处理大规模数据时可能会消耗大量内存和计算资源
计算方式
将连续的曲线离散化为一系列点集。这一步是将曲线(P)和(Q)分别用一组离散点表示
构建距离矩阵(D)
距离矩阵(D)的元素(D(i, j))表示曲线(P)上第i个点$(P_i)$和曲线(Q)上第j个点$(Q_j)$之间的欧几里德距离$D(i, j)= | P_i - Q_j |$
最终矩阵(C)的右下角元素(C(n-1, m-1))即为曲线(P)和曲线(Q)之间的Fréchet距离
动态规划矩阵的填充步骤
动态规划矩阵(C)的尺寸与距离矩阵(D)相同,大小为 $n \times m$ ,其中(n)和(m)分别是曲线(P)和曲线(Q)的离散点数。
初始条件:$C(0, 0) = D(0, 0)$ ,表示从(P)和(Q)的起点出发时的距离
对于第一行和第一列
$$
C(i, 0) = \max(C(i-1, 0), D(i, 0)) \quad \forall i \geq 1
$$$$
C(0, j) = \max(C(0, j-1), D(0, j)) \quad \forall j \geq 1
$$对于其他,使用如下递推公式
$$
C(i, j) = \max\left( D(i, j), \min\left( C(i-1, j), C(i, j-1), C(i-1, j-1) \right) \right)
$$
解释上述公式:
- $D(i, j)$是曲线(P)上的第(i)个点和曲线(Q)上的第(j)个点之间的欧几里德距离。
- $\min(C(i-1, j), C(i, j-1), C(i-1, j-1))$表示从之前的状态转移到当前状态的最小Fréchet距离。
- $\max$确保当前状态的Fréchet距离考虑了当前点之间的距离。
这样计算的每一步都确保了Fréchet距离考虑了曲线上的所有点对点距离,同时保持了路径的连贯性和正确性。
通过动态规划的方法,我们逐步计算和记录了从曲线起点到各个点之间的Fréchet距离,确保考虑到曲线的全局形状和相似性。这种方法在理论上和实际应用中都被证明是有效的。
动态规划表格的实际构建演示
下面是一个示例,假设我们有两个离散化的曲线(P)和(Q ),它们的点集分别为(P = {P_0, P_1, P_2})和(Q = {Q_0, Q_1} ),对应的距离矩阵(D)和动态规划矩阵(C)的构建过程如下:
计算距离矩阵(D)
初始化动态规划矩阵(C)
填充第一行和第一列
使用递推公式填充其余部分
$$
C(1, 1) = \max(D(1, 1), \min(C(0, 1), C(1, 0), C(0, 0)))
$$$$
C(2, 1) = \max(D(2, 1), \min(C(1, 1), C(2, 0), C(1, 0)))
$$最终,我们得到填充完的动态规划矩阵(C)
最终得到曲线(P)和(Q)的Fréchet距离为C(2,1)
递归实现代码案例
这个代码可以计算元素个数不同的两个序列的相似度
1 | //版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 |
曲线抽稀
在处理矢量化数据时,记录中往往会有很多重复数据,对进一步数据处理带来诸多不便。多余的数据一方面浪费了较多的存储空间,另一方面造成所要表达的图形不光滑或不符合标准。因此要通过某种规则,在保证矢量曲线形状不变的情况下, 最大限度地减少数据点个数,这个过程称为抽稀。
通俗的讲就是对曲线进行采样简化,即在曲线上取有限个点,将其变为折线,并且能够在一定程度保持原有形状。比较常用的两种抽稀算法是:
- 道格拉斯-普克(Douglas-Peuker)算法 效率更高,主流做法
- 垂距限值法
优劣
- 对简化精度要求较高且数据量不大,垂距限值法可能更合适;
- 对于大规模数据或需要快速处理的情况,Douglas-Peucker算法则更为优越。
阈值越高,抽稀后越平滑
除了这两套算法外,还有如下方式:
基于时间间隔的抽稀:
如果你的数据是基于时间产生的,使用一定的时间窗口对数据进行采样。例如,每1秒显示一个数据点。当数据增加到一定程度时,你可以调整窗口,增加每次采样的时间间隔(比如从1秒变成5秒)。这样可以避免在图表上显示过多数据点。
基于像素密度的抽稀:
对于每个像素宽度,只保留一个数据点。可以通过计算当前图表宽度上的像素数,并动态调整你显示的数据点数量。比如当图表只有100个像素宽时,你可以从原始数据中选择100个代表性点。
Douglas-Peucker算法:
该算法用于线简化,通过去除不重要的点来减少数据。Douglas-Peucker算法会从一条折线中移除那些不会显著改变曲线形状的点,从而降低点的密度。适合用于有曲线的图表。
指数采样:
根据数据点的数量,使用指数抽稀策略。比如,当数据点少于100个时,保持全部显示。当数据点超过100个时,只显示每2个数据点中的一个;当数据点超过1000时,显示每4个数据点中的一个,依此类推。
关键点保留策略
在进行抽稀时,确保保留关键点,例如局部极值点(峰值和谷值)、转折点或数据斜率变化剧烈的点。这可以通过检测局部变化来实现,如果某点相对于前后的点有明显的变化,标记它为关键点并保留。比如使用二阶差分或曲率判断是否为关键点。
Douglas-Peucker算法(线简化算法)
该算法通过递归划分折线,保留那些对线条形状影响较大的点,并删除对整体形状影响较小的点。这有助于保持数据的形状特征,同时减少点数。Douglas-Peucker算法的优点是可以通过调整容差来控制抽稀后的精度。
自适应采样
根据数据的变化速率或斜率来调整采样频率。在平滑或变化较慢的区域,可以稀疏采样,而在数据变化剧烈的区域,保留更多的点。例如,当检测到数据变化较大时,动态减少抽稀的频率,确保保留细节。
多分辨率展示
保持多层次的数据抽样结果。例如,绘制时可以使用较稀疏的抽样数据来保证性能,而在用户缩放或平移到某个区域时,动态加载和显示该区域的详细数据。这样可以在保证整体形状的同时,提供详细的局部信息。
滑动窗口平滑法
在保留原始数据点形状的基础上,你可以在抽稀过程中应用滑动窗口平滑法。这种方法能够保留整体形态,并减少噪声引起的小幅波动。滑动窗口可以随着数据点的密度自适应调整大小。
保留首尾点
在抽稀过程中,始终保留数据的起点和终点,确保曲线的整体趋势不会丢失。这有助于在大幅抽稀的情况下保持数据的宏观走势。
窗口缩放:
如果你的图表支持平移和缩放功能,可以让用户通过缩放来查看更多细节。当缩小时,显示较少的数据点,而当放大时,展示更多的原始数据。
动态抽样比例调整:
根据图表的渲染性能动态调整抽稀比例。可以定期测量绘制速度和响应时间,如果发现绘制过慢,就增加抽稀率。这样保证在不同设备上都能有流畅的绘图体验。
Douglas-Peucker算法
道格拉斯普克(Douglas-Peuker)算法(通常简称为 DP 算法)是一种用于曲线抽稀(简化曲线)的方法,是线状要素抽稀的经典算法。用它处理大量冗余的几何数据点,既可以达到数据量精简的目的,又可以在很大程度上保留几何形状的骨架。
Douglas-Peucker 算法的步骤通常如下:
- 连接曲线首尾两点A、B;
- 依次计算曲线上所有点到A、B两点所在曲线的距离(即作垂线,垂线的长短);
- 计算最大距离D,如果D小于阈值threshold,则去掉曲线上除A、B外的所有点;如果D大于阈值threshold,则把曲线以最大距离分割成两段;
- 对所有曲线分段重复1-3步骤,直到所有D均小于阈值。即完成抽稀
这种算法的抽稀精度与阈值有很大关系,阈值越大,简化程度越大,点减少的越多;反之简化程度越低,点保留的越多,形状也越趋于原曲线。
此处附一个计算点到直线距离的代码: [[数学#点到直线的距离|数学推导参考此处]]
2
3
4
5
6
7
8
9
10
11
12
13
14
// 计算点 C(x3, y3) 到直线 AB 的距离
double pointToLineDistance(double x1, double y1, double x2, double y2, double x3, double y3) {
// 计算直线 AB 的参数 A, B, C
double A = y2 - y1; // 直线的 A
double B = x1 - x2; // 直线的 B
double C = x2 * y1 - x1 * y2; // 直线的 C
// 使用距离公式计算点 C 到直线 AB 的距离
double distance = fabs(A * x3 + B * y3 + C) / sqrt(A * A + B * B);
return distance;
}

通过这种方式,Douglas-Peucker 算法能够有效地减少曲线的复杂度,同时尽量保留曲线的形状特征,广泛应用于计算机图形学、地理信息系统(GIS)等领域。
在opencv中,轮廓近似函数:cv2.approxPolyDP(cnt, eps,True)由Douglas-Peuker算法实现
案例
1 |
|
由于DP算法中的阈值需要人工手动设定,因此此处记录一个自适应DP算法
可以根据垂比弦值来量化节点的重要性
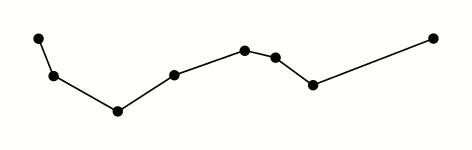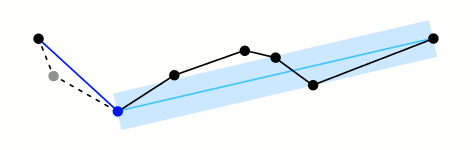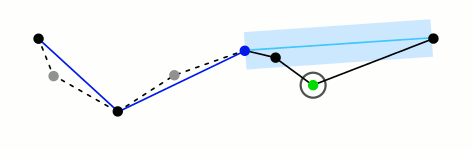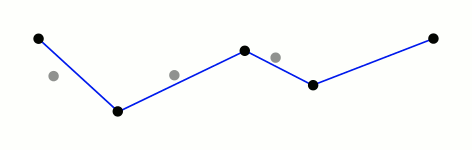
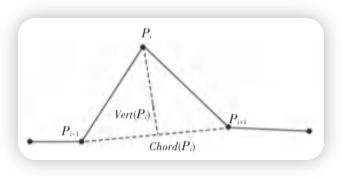
$$
importance(P_{i})=\frac{Vert(P_{i})}{Chord(P_{i})}
$$
节点的重要值衡量了该节点对整个矢量图形维持原形状的重要性,重要值越大,该节点对原图形形状越重要。 为了使压缩后的矢量图形尽可能地维持原图形形状,就需要保留这些重要值很大的节点然后引入了角度变化率(指的是拟合曲线上相邻两点切线方向上角度的变化率),用于局部计算阈值’
粗略提取了一些思想,整体算法较为复杂,涉及到曲线拟合,暂略
垂距限值法
垂距限值法是一种简单的轨迹平滑算法,用于将给定的轨迹进行简化,从而减少轨迹的噪声,并减少机器人的运动轨迹。该算法的基本思想是对轨迹上的每个点进行垂线投影,如果垂线的长度小于某个阈值,则认为该点是不必要的,可以将其删除,从而实现轨迹的简化。
算法原理
- 以第一个点开始,计算第一个点到前一个点和后一个点所在直线的垂距;
- 如果垂距小于阈值,则保留该点,并将其作为下一个点计算;
- 如果垂距大于阈值,则舍弃该点,并将下一个点作为当前点重新进行计算;
- 依次类推,直到计算完最后一个点。
1 | // 计算垂距 |
这里罗列一个C#算垂距的例子
1 | static long DateTimeToLong(DateTime dateTime) |
曲线趋势中心点
整体思路如下:
- 准备数据:排序、平滑
- 定义度量:设计误差函数,确定采样策略
- 粗搜索:大范围低精度扫描
- 细搜索:小范围高精度定位
- 结果验证:计算对称评分,可视化检查
- 输出:返回最佳X值及相关指标
详细参考如下:
去噪,突出整体趋势,减少噪声对对称性判断的影响(移动平均/低通滤波/高斯滤波/样条拟合)
定义对称性度量
定义一个函数(误差函数)来量化曲线关于某个中心点x_c的对称程度
核心思路
对于候选中心点X_c,曲线左右对称意味着:
- 对于任意偏移量d
- 左侧点(X_c - d)的Y值 ≈ 右侧点(X_c + d)的Y值
误差函数设计
- **均方误差(MSE)**:
- 计算所有偏移量d对应的(Y_left - Y_right)²
- 求这些平方差的平均值
- 优点:对大误差更敏感,能更好区分对称性程度
- **平均绝对误差(MAE)**:
- 计算所有偏移量d对应的|Y_left - Y_right|
- 求这些绝对差的平均值
- 优点:对异常值不敏感
偏移量采样策略
- d_max确定:取X_c到左边界和右边界距离的较小值
- 采样点数量:通常在50-100个点之间平衡精度和效率
- 采样方式:均匀分布在[0, d_max]区间
搜索候选中心点
分层搜索策略
- 粗搜索阶段:
- 目的:快速定位大致区域
- 方法:将整个范围分成50-100个等距点
- 计算每个点的对称误差
- 记录误差最小的点作为初步中心
- 细搜索阶段:
- 目的:在粗搜索结果附近精确查找
- 方法:在粗搜索最佳点周围小范围内密集采样
- 范围设置:通常取粗搜索步长的2倍为半径
- 采样密度:比粗搜索高5-10倍
- 粗搜索阶段:
插值处理
为什么需要插值
- 数据点是离散的,但对称点可能不在原始数据点上
- 需要估计任意X位置的Y值
插值方法选择
边界处理
- 当X超出数据范围时,返回无效值或使用外推法
- 在算法中应跳过这些点,不参与误差计算
优化策略
效率优化
- 采样点优化:
- 在平坦区域减少采样密度
- 在变化剧烈区域增加采样密度
- 并行计算:
- 粗搜索中各候选点可并行计算误差
- 细搜索中各点也可并行处理
- 提前终止:
- 当找到明显低误差点时停止搜索
- 但需设置合理阈值防止局部最优
精度优化
- 迭代细化:
- 在细搜索结果基础上再次缩小范围搜索
- 可进行多轮迭代提高精度
- 动态步长调整:
- 根据误差变化率调整搜索步长
- 误差变化大时用小步长,变化平缓时用大步长
- 采样点优化:
结果评估与输出
对称性评分
- 计算方法:1 - (实际误差/最大可能误差)
- 意义:0-1之间的值,越接近1对称性越好
- 用途:判断结果可靠性,过滤低质量结果
多峰处理
当发现多个局部最优解时:
- 记录所有候选点
- 根据对称性评分排序
- 返回最佳点或所有候选点供用户选择
结果验证
- 可视化:绘制对称轴和原始曲线对比
- 统计检验:计算左右两侧的相关系数
- 残差分析:检查误差分布是否随机
特殊场景处理
非理想对称曲线
整体趋势处理:
方法:先去除线性或多项式趋势
前提是如果需要去除整体趋势影响的干扰才考虑这样处理,若趋势本身就是对称的一部分,在这情况下,可以跳过此步骤。
步骤:
- 拟合整体趋势线
- 原始数据减去趋势值
- 在残差数据上找对称中心
部分对称处理:
- 指定关注区间而非整个曲线
- 在局部区域应用相同算法
噪声处理进阶
- 鲁棒统计方法:
- 使用中位数代替平均值
- 忽略一定比例的异常点
- 多尺度分析:
- 在不同平滑程度上分别计算
- 综合多个尺度的结果
无解情况处理
- 当最小误差仍很大时:
- 返回”未找到有效对称中心”
- 提供可能原因分析(如数据噪声大、曲线不对称)
数值分析:曲线拟合算法和函数逼近
与插值方法最大的区别在于最终要得到具体的函数关系
在数值积分中,除了使用梯形简单计算积分外,还可以使用插值或拟合技术来构造多项式来逼近被积函数。这里简单介绍一下常用的方法:
- 插值法:插值法通过已知数据点来构造通过这些点的多项式函数。常见的插值方法包括拉格朗日插值和牛顿插值。在辛普森法则中,我们可以通过子区间的左端点、右端点和中点处的函数值来构造一个二次多项式,从而近似代替被积函数。
- 拟合法:拟合法通过已知数据点来拟合一个多项式函数,使得这个多项式函数与原函数在这些点上尽可能接近。常见的拟合方法包括最小二乘法和最小二乘多项式拟合。在数值积分中,我们可以使用拟合技术来构造一个简单的多项式函数来逼近被积函数。
动态时间归整
DTW(Dynamic Time Warping)
按照距离最近的原则,构建两个序列中的元素之间的对应的关系,用于评估两个序列的相似性。
应用场景:
计算两个序列之间的相似性
动作识别:传感器x,y,z的加速度和角速度6维数据作为一组数据,评估运动的相似性
获取匹配特征对(最终取路径)
声音转换,源说话人的语音转换为目标说话人的特征需要先配对,才能构造转换函数
语音识别: 文本和语音特征对齐 (距离计算要提前训练一个DNN的深度神经网络的分类器(输入的是特征,输出的是音素概率),使用最终输出的概率值作为距离)
股市交易曲线匹配
DNA碱基序列匹配
非常多应用场景
要求:
- 单向对应,不能回头
- 一一对应,不能有空
- 对应之后,距离最近

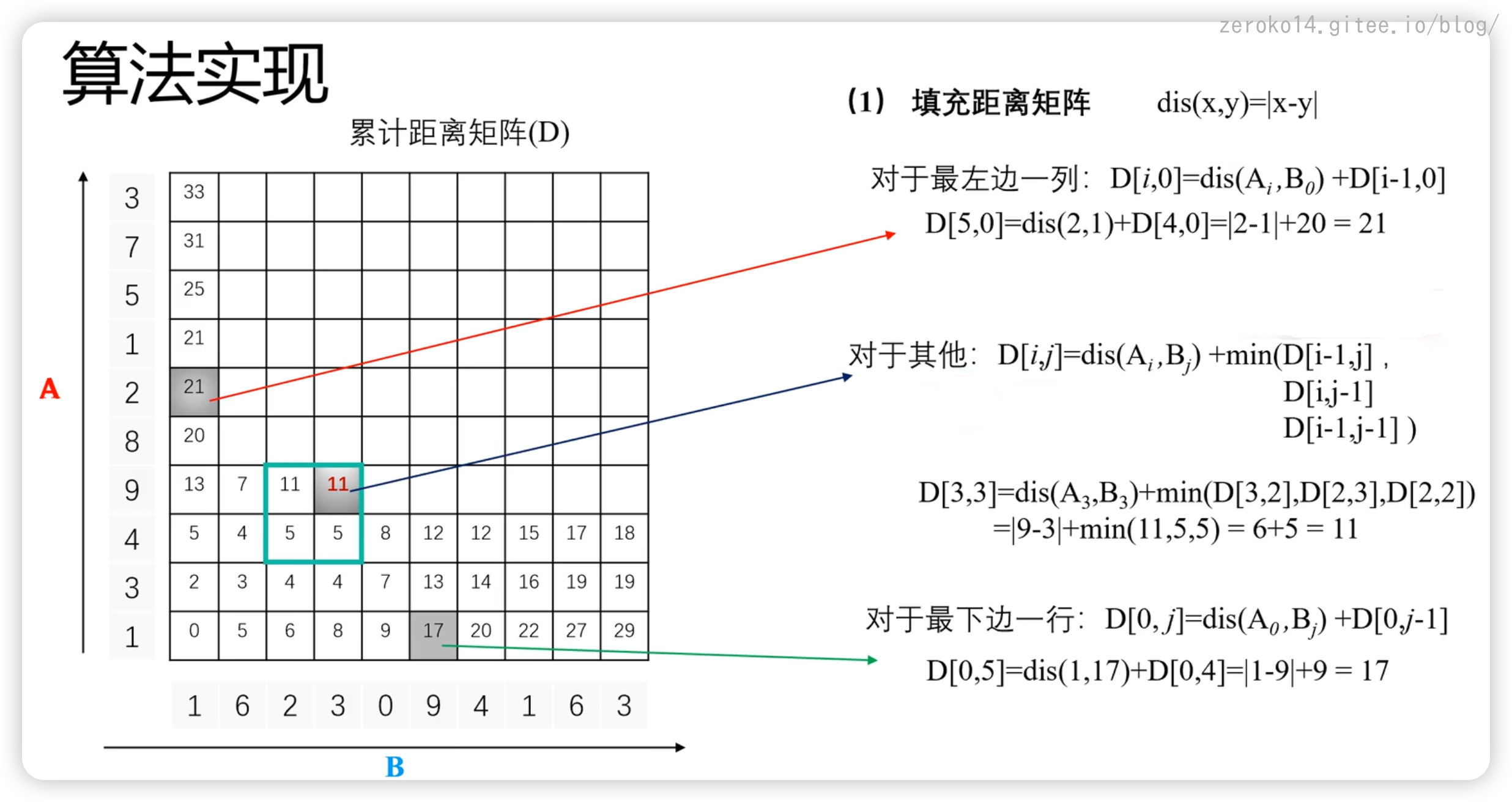
定义一个距离公式,怎么定义都可以,比如说最简单的: dis(x,y)=|x-y|
假设有A,B两个序列,A序列有m个元素,B序列有n个元素,将会产出一个mn的*累计距离矩阵(D)
填充算法遵循如下公司
对于最左边的一列:
$$
\mathrm{D}[i,0]=\mathrm{dis}(\mathrm{A}_i,\mathrm{B}_0)+\mathrm{D}[i-1,0]
$$对于最下面的一行:(实际上算法与上面一样,方向变了而已)
$$
\mathrm{D}[0,j]=\mathrm{dis}(\mathrm{A}_0,\mathrm{B}_j)+\mathrm{D}[0,j-1]
$$对于其他元素
$$
\begin{array}{c}\mathrm{D}[i,j]=\mathrm{dis}(\mathrm{A}_i,\mathrm{B}_j)+\mathrm{min}(\mathrm{D}[\mathrm{i}-1,\mathrm{j}] ,\mathrm{D}[\mathrm{i},\mathrm{j}-1],\mathrm{D}[\mathrm{i}-1,\mathrm{j}-1] )\end{array}
$$
为什么是左下三个点呢?原因是因为一对一
矩阵被填充完毕后,从右上角开始,向左下找寻配准路径找到左下三点中,较小的那个作为下一节点。
如图:
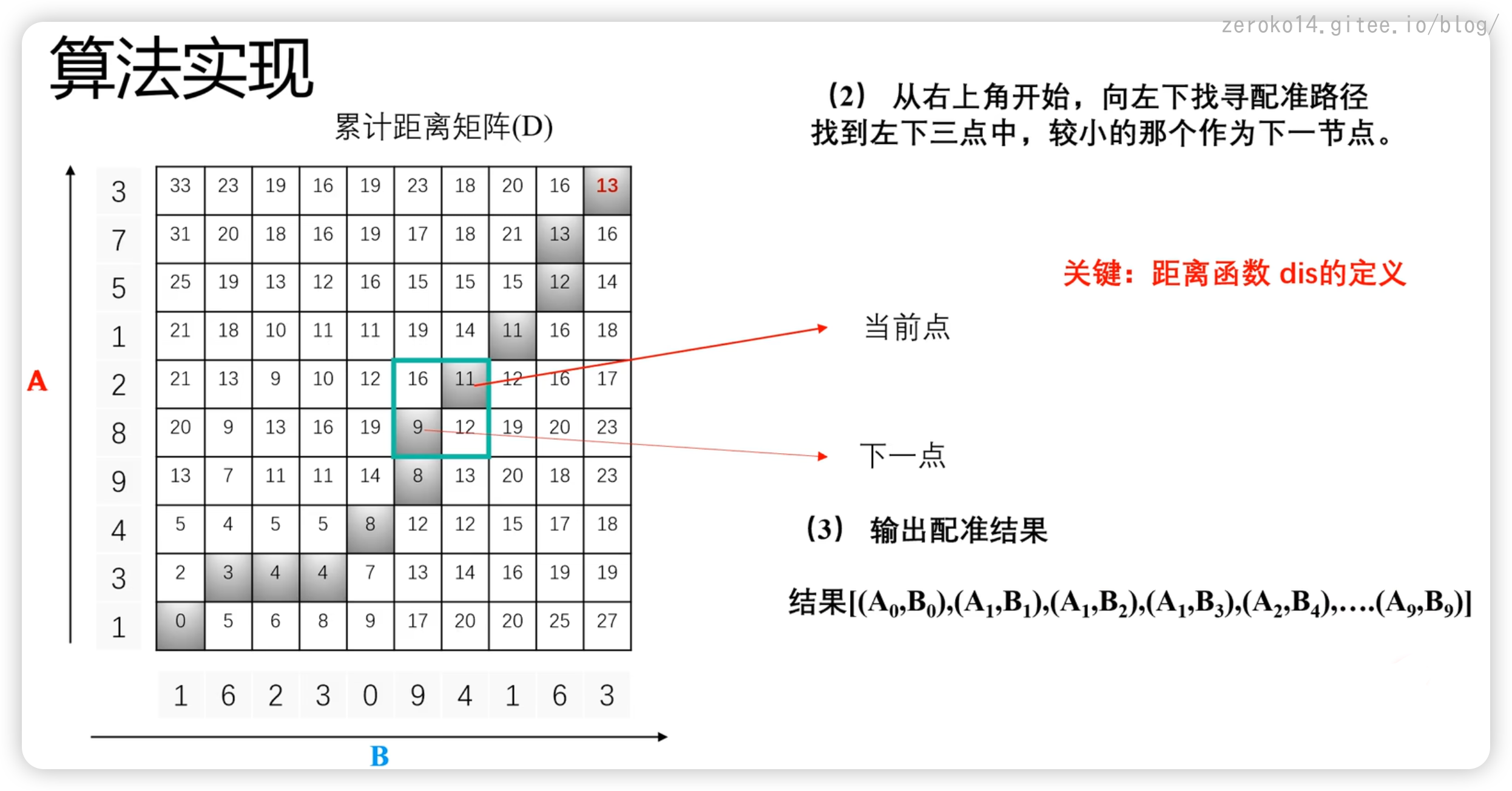
最终就能得到配准结果
完整过程参考该视频👇🏻
实际计算的过程中,只需要利用动态规划的思想就可以实现,并不需要填充矩阵
离群点/异常点查找算法
异常就是偏离数据主要分布的点或者群体,导致异常的原因有很多,比如恶意行为,系统故障,蓄意欺诈等,
因此,异常检测对于决策系统是必须的。
离群点/异常点介绍
异常点分类
单点异常
个体数据实例相对于其余数据被视为异常(例如交易流水中的大额交易)
上下文异常(时间序列)
一般是在有时间的序列集中才存在,仅在特定上下文中异常,单拿出来看不出异常
集体异常(连续性异常)
相关数据实例的集合相对于整个数据集是异常的,对于单个值则不是
两种可能性
- 按无法预料的顺序发生
- 值的组合是无法预料的
难点
- 大部分情况下数据是没有标签(label)的,各种成熟的监督学习(supervised learning)没有用武之地。
- 区分噪音(noise)和异常点(anomaly)时难度很大,甚至需要发挥一点点想象力和直觉。
- 当多种诈骗数据混合在一起,区分不同的诈骗类型更难。根本原因还是因为我们并不了解每一种诈骗定义。
异常检测算法的分类
时序相关 vs 时序独立
数据的变化是否依赖于时间维度
全局 vs 局部
每个点的参考对象是全局的点,还是仅参考周围的点
标签 vs 异常分数
算法检测结果的输出形式不同
异常分数可以对异常程度进行排序
基于模型特性
根据异常点的特性,采用不同的算法直接建模
时序相关下的异常检测:
滑动窗口
根据不同场景,可以选择 Moving Average 或 Expanding MAD 等组合进行计算
马尔科夫链
可用马尔科夫链来测时间序列发生的概率,从而检测到那些发生概率低的异常序列
时间序列聚类
采用 DTW 的方式计算不同时间序列间的距离,减弱时间差的影响,检测出那些高度相似的时序群组
时序预测方法
通过对已有时序的预测,评估预测值与实际值的偏差是否过大,从而判断某个时间点是否存在异常
异常检测的经典思想模型
这里提到的经典思想模型,很少拿来直接使用,但如今常用的流行算法都是基于这些原始模型的思想衍生出来的
统计检验方法
基本假设:正常的数据遵循特定的分布形式,并占了很大比例,异常点的位置较正常点范围存在较大偏移。
存在的问题往往是: 均值和标准差都对异常值很敏感,在实际计算的时候,异常值也被包含在全部数据集里
基于偏差的方法
给定一个数据集(可以为局部子集或全局点集),若一个点自身的值与整个集合的指标有过大的偏差,则该点为异常点。去除掉这个点后,整个集合的方差会减小。
基本假设: 数据集最外围的点为异常点
模型思想:定义一个指标 SF(smooth factor),它表示当某个点从集合移除掉后,方差( variance )降低的值。[Arning et al. 1996]
基于距离的方法
计算每个点与周围点的距离,来判断该点是否为异常点。
基本假设:正常点的周围存在多个近邻点,而异常点分布在稀疏区域,距离周围点的距离较远。
DB 模型:给定半径r和比例 T,假设对 p点进行检测,若与p点距离小于半径r的点数对于全部点数的比例低于 T,则该点为异常点。

基于密度的方法
对比目标点的周围密度与其近邻点的周围密度,基于两个密度值计算出相对密度,作为异常分数。
基本假设:正常点与其近邻点的密度是相近的,而异常点的密度与其近邻点存在较大的差异。
开发该方法的动机:基于距离的异常检测方法无法处理密度不同的情况。针对右图,若采用 DB model,半径和比例固定,02 会被识别为异常点,而C1 子集中的很多点的距离都比02小,也就会被识别为正常点。若引入密度作为标准,就会有不同的检测结果。
解决方法:引入相对密度
深度学习方法–Autoencoder
Autoencoder,即自编码器,是一种无监督学习模型,包含两个部分:encoder(编码器)和 decoder(解码器)。
Encoder 用来发现给定数据的压缩表示,decoder 用来重建原始输入。在训练时,decoder 强迫 autoencoder 选择最有信息量的特征,最终保存在压缩表示中。最终压缩后的表示就在中间的 coder 层中。

方法盘点
有如下方法:
- 统计方法
- Z-score(标准分数):计算数据点距离均值的标准差数,通常z-score超过3或小于-3的点被认为是异常点。
- IQR(四分位距):计算数据的四分位数(Q1和Q3),然后计算IQR = Q3 - Q1。通常定义在Q1 - 1.5 * IQR以下或Q3 + 1.5 * IQR以上的点为异常点。
- Grubbs’ Test:用于检测单变量数据集中的单个异常值。该测试假设数据呈正态分布。
- 基于距离的方法
- K-均值聚类:在进行K-均值聚类后,距离其最近质心最远的点可以被认为是异常点。
- DBSCAN(基于密度的聚类):该方法可以找出密度较低区域中的点,认为它们是异常点。
- LOF(局部离群因子):基于密度的局部异常值检测方法,通过比较点与其邻居的局部密度来判断是否是异常点。
- 机器学习方法
- 孤立森林(Isolation Forest):基于树的随机森林方法,通过随机分割数据来检测异常点。
- One-Class SVM:一种支持向量机方法,适用于异常检测。
- 自编码器(Autoencoder):一种神经网络方法,通过重构误差来检测异常点。
- 基于概率的方法
- 高斯混合模型(GMM):通过拟合数据的多峰分布来识别异常点。
- 贝叶斯方法:通过计算数据点的概率分布来检测异常点。
- 可视化方法
- 箱线图(Box Plot):通过箱线图可以直观地看到异常点。
- 散点图(Scatter Plot):特别适合二维数据,通过观察数据点的分布情况来发现异常点。
结合滑动窗口动态检测异常点


下面罗列几种方法
四分位距法
先要获取到完整的数据序列,才能处理
四分位距法(Interquartile Range, IQR)是一种统计方法,用于衡量数据的离散程度。它通过计算数据的上四分位数(Q3)和下四分位数(Q1)之间的差值来描述数据的分散程度。
具体步骤如下:
- 首先,将数据按大小顺序排列。
- 然后计算数据的上四分位数(Q3)和下四分位数(Q1)。
- 上四分位数(Q3)是将数据分成四等份后,位于第三份的数值。
- 下四分位数(Q1)是将数据分成四等份后,位于第一份的数值。
- 计算四分位距(IQR):IQR = Q3 - Q1。
- 根据IQR的大小,可以判断数据的离散程度:
- 如果某个数据点小于Q1 - 1.5 * IQR或大于Q3 + 1.5 * IQR,则可以被视为异常值(离群值)。
四分位距法相对于标准差等其他离散度量具有一定的优势,因为它对异常值的影响较小,更能反映数据的真实分布情况。在数据分析和异常值检测中,四分位距法常被用于识别离群值。
代码:
1 | private static double GetPercentile(List<double> sortedData, double percentile) |
Z-score
Z-score方法是一种常用的统计方法,用于衡量数据点与数据集均值之间的差异,即数据点距离均值的标准差数。Z-score可以帮助我们判断数据点在数据集中的相对位置,从而进行比较和分析。
缺陷:因涉及到均值,对异常点相对敏感
[[数学#标准差|标准差参考]]
Z-score的计算公式如下:
$$
Z = \frac{x - \mu}{\sigma}
$$
其中,Z表示Z-score,x表示数据点的数值,μ表示数据集的均值,σ表示数据集的标准差。
通过计算Z-score,我们可以将数据标准化为标准正态分布,即均值为0,标准差为1的分布。在标准正态分布中,大约68%的数据点落在±1个标准差范围内,约95%的数据点落在±2个标准差范围内,约99.7%的数据点落在±3个标准差范围内。
通常情况下,Z-score超过3或小于-3的数据点被认为是异常值。Z-score方法适用于数据符合正态分布的情况,可以帮助我们识别和处理数据中的异常值,并进行数据分析和统计推断。
$$
正常范围:-3<=Z<=3
$$
也可以这么理解
$$
某个值处于正常范围:(某个值-平均值)的绝对值<=3倍标准差
$$
代码:
1 | /// <summary> |
箱线图法
箱线图法是一种可视化离群值/异常值的有效方法
箱线图(Box Plot)是一种用于显示数据分布情况的统计图表,能够直观地展示数据的中位数、上下四分位数、最大值、最小值以及离群点。箱线图通常包含以下几个要素:
箱体(Box):箱体代表数据的四分位数范围,即数据的中间50%。箱体上边界表示数据的上四分位数(Q3),下边界表示数据的下四分位数(Q1),箱体内部的线表示数据的中位数。
触须(Whiskers):触须延伸自箱体,用于显示数据的最大值和最小值。触须的长度通常是箱体高度的1.5倍的距离,超出该距离的数据点被认为是异常值。
离群点(Outliers):箱线图中的离群点是指远离箱体的个别数据点,它们可能是数据中的异常值。离群点通常被标记出来,帮助我们识别数据中的异常情况。
孤立森林算法
属于机器学习算法
孤立森林(isolation Forest)算法,2008年由刘飞、周志华等提出,算法不借助类似距离、密度等指标去描述样本与其他样本的差异,而是直接去刻画所谓的**疏离程度(isolation)**,因此该算法简单、高效,在工业界应用较多。
一种集成模型,线性时间复杂度,可以用来处理大规模数据集
孤立森林通过构建随机二叉树来快速识别异常点,其效率得益于随机化过程和树结构的特性。由于它不需要假设数据的分布或异常点的比例,因此在处理大规模数据集和高维数据时表现出色。此外,由于算法的并行性,它还可以很好地利用多核处理器进行加速。
适用情况
- Isolation Forest在数据量比较大的情况下效果更好
- 一般来说,异常值在数据集中占的比例较小,通常是1%到5%。Isolation Forest能较好地处理这种低比例异常值的情况。
理解
孤立森林(Isolation Forest)是一种基于树的无监督学习算法,用于异常检测。它的核心思想是异常点更容易被孤立(隔离)出来。以下是孤立森林算法的详细原理:
孤立森林通过随机选择一个特征并在特征的随机值上切分数据,构建多棵树(称为孤立树)。它利用树的深度来测量数据点的孤立程度:深度越浅,越容易被孤立,越可能是异常点。
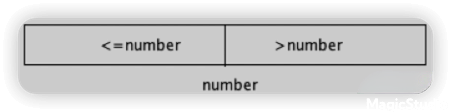
用一个例子来说明孤立森林的思想:假设现在有一组一维数据(如下图),我们要对这组数据进行切分,目的是把点A和 B单独切分出来,先在最大,值和最小值之间随机选择一个值 X,然后按照 <X 和 >=X 可以把数据分成左右两组,在这两组数据中分别重复这个步骤,直到数据不可再分。
点B跟其他数据比较疏离,可能用很少的次数就可以把它切分出来,点 A 跟其他数据点聚在一起,可能需要更多的次数才能把它切分出来。
那么从统计意义上来说,相对聚集的点需要分割的次数较多,比较孤立的点需要的分割次数少,孤立森林就是利用分割的次数来度量一个点是聚集的(正常)还是孤立的(异常)。

- 随机选择特征和随机切割:孤立森林通过随机选择一个特征和一个随机切割值来构建二叉树。该过程重复进行,直到每个样本点都被孤立在叶子节点。
- 异常值定位:由于异常值更容易被孤立,因此异常值通常在树的较浅层被划分出来。通过路径长度可以衡量样本点在树中的孤立程度,路径长度越短,则样本点越可能是异常值。
- 异常得分计算:根据样本点在多棵树中的平均路径长度来计算异常得分。路径长度越短,异常得分越高,反之则越低。
对于未曾见过的新数据点,将其在孤立森林(训练好的)中的每棵孤立树中进行路径长度的计算。
计算路径长度的方法是:从根节点开始,根据节点的分割特征和分割值,确定数据点进入左子树还是右子树,直到到达叶子节点,记录经过的节点数,即为路径长度。
对新数据点在多棵孤立树中的路径长度取平均值。
如果平均路径长度明显短于正常数据在孤立森林中的平均路径长度,那么就可以认为这个新数据点可能是异常的
具体步骤
随机选择特征和切分点:
- 对于每棵树,从数据集中随机选择一个特征,并在该特征的范围内随机选择一个切分点。
- 递归地对每个分区重复此过程,直到达到预定的树深度或节点包含的样本数量小于等于1。
构建孤立树:
- 孤立树是通过不断随机选择特征和切分点来构建的二叉树。
- 每个节点对应一次数据的分裂,分裂点是根据选定特征的随机切分点。
计算路径长度:
- 对于每个数据点,计算其在孤立树中从根节点到达叶节点的路径长度。
- 路径长度较短的数据点更容易被孤立,通常被认为是异常点。
异常得分计算:
孤立森林利用多棵孤立树来稳定路径长度的估计。
异常得分是基于平均路径长度计算的,通常归一化到0到1之间。
计算公式:
$$
s(x,n)=2^{-\frac{E(h(x))}{c(n)}}
$$
其中,𝐸(ℎ(𝑥))是数据点𝑥x在孤立森林中的平均路径长度,𝑐(𝑛)是一个常数,用于标准化路径长度。常数𝑐(𝑛)的计算
𝑐(𝑛)是用于标准化路径长度的常数,定义如下:
$$
c(n)=2H(n-1)-\frac{2(n-1)}n
$$
其中,𝐻(𝑖) 是第𝑖个调和数
$$
H(i)=\ln(i)+0.5772156649\text{(欧拉-马歇罗尼常数)}
$$
实现代码
注意:下面的代码可以针对多维数据,采用的数据存储容器是List<List<double>>
定义节点类
1 | // 定义孤立森林中的树节点类 |
构建孤立树
归方法构建孤立树。
1 | // 定义孤立森林中的单棵树构建逻辑 |
计算路径长度
实现一个方法来计算数据点在孤立树中的路径长度。
1 | // 定义一个方法来计算从根节点到特定数据点的路径长度,这是孤立森林算法中的一部分。 |
计算异常得分
注意:异常得分越高,越异常
实现一个类来封装整个孤立森林算法,包含训练和预测方法。
1 | // 定义孤立森林类,用于异常检测 |
使用孤立森林算法
1 | // 示例数据,二维数组,每行代表一个样本 |
一维孤立森林完整代码
下面附带一个完整版的一维孤立森林算法,更方便理解
1 | using System; |
添加并行处理的一维孤立森林代码
- 并行化建树过程:使用
Parallel.For来并行构建多棵孤立树,提高了建模过程的效率。 - 并行化计算异常得分:在计算异常得分时,使用
Parallel.For来并行处理每个数据点,从而加速了异常检测过程。
1 | using System; |
适用场景
常用于网络流量异常检测、工业故障检测等领域
网络流量异常检测
首先,对网络流量数据进行特征提取,例如数据包大小、流量速率、协议类型、源和目的 IP 地址等。然后将这些特征数据输入到孤立森林模型中。正常的网络流量模式往往具有相似的特征,需要较多的分割才能被孤立;而异常的流量,如 DDoS 攻击、非法访问等,由于其特征与正常流量差异较大,可能在孤立树中较浅的层次就被孤立出来。通过分析数据点在孤立森林中的路径长度,可以判断其是否为异常流量。
工业故障检测
在工业故障检测方面,例如对于一条生产线,收集诸如设备温度、压力、转速、能耗等参数作为特征。正常运行时,这些参数会在一定范围内稳定变化,形成一种常见的模式。当出现故障时,某些参数可能会偏离正常范围。将这些参数数据输入孤立森林模型,故障状态所对应的特征组合可能更容易被孤立,从而被检测为异常,实现故障的早期发现和预警。
其他更高级的算法
DNN(Deep Neural Network):
- 原理:DNN是一种深度学习模型,由多个隐藏层组成的神经网络。它通过学习数据的复杂非线性关系来进行异常检测。
- 优点:DNN可以学习数据中的高阶特征和复杂模式,适用于处理大规模、高维度的数据集。
- 缺点:DNN需要大量的标记数据进行训练,且模型复杂度高,训练时间长。
OneClass-SVM(One-Class Support Vector Machine):
- 原理:OneClass-SVM是一种支持向量机模型,用于从单一类别的数据中学习正常样本的边界,然后识别与正常样本差异较大的异常点。
- 优点:OneClass-SVM不需要异常点的标记数据,只需要正常样本进行训练,适用于非常规数据集的异常检测。
- 缺点:OneClass-SVM对参数的选择敏感,可能需要调优。
AutoEncoder(自编码器):
- 原理:AutoEncoder是一种神经网络模型,用于学习数据的压缩表示,然后重构输入数据。异常点通常在重构误差较大的数据点中被识别为异常。
- 优点:AutoEncoder可以自动学习数据的特征表示,适用于无监督学习的异常检测。
- 缺点:AutoEncoder的性能受到数据分布的影响,对于高度非线性的数据集可能表现不佳。
回归分析
在统计学中,回归分析是一种用来探讨一个或多个自变量与因变量之间关系的方法。回归分析旨在了解自变量对因变量的影响程度,以及预测因变量的数值。回归分析可以帮助我们理解变量之间的关联性,并用于预测和解释数据。
曲线拟合和回归分析都是统计学中常用的方法,用于探索变量之间的关系。曲线拟合是指通过拟合一个数学模型来描述变量之间的关系,通常用于找到最能代表数据分布的曲线或函数。而回归分析则是一种更广泛的方法,用于研究自变量与因变量之间的关系,并通过建立回归方程来预测或解释因变量的数值。
在某些情况下,曲线拟合可以被看作是回归分析的一种特例,特别是当我们试图拟合一个曲线来描述自变量和因变量之间的关系时
线性拟合
线性拟合是一种统计学和数学中常用的方法,用于找到一条最佳拟合直线来描述两个变量之间的关系。在线性拟合中,我们尝试找到一条直线,使得该直线与数据点的残差(实际观测值与拟合值之间的差异)之和最小
性拟合通常用于分析两个变量之间的线性关系,例如通过一组数据点来找到最佳拟合直线,以便预测未来的数值或者对数据进行建模。线性拟合的目标是找到最佳拟合直线的斜率和截距,以最好地描述数据点之间的关系。
最小二乘法
1 | /// <summary> |
图算法
- DFS 深度优先搜索
- BFS 广度优先搜索

BFS 可以用来求最短路径问题
DFS 常用来处理全排列问题
这里提一嘴:深度优先遍历、递归、栈,它们三者的关系,我个人以为它们背后统一的逻辑都是「后进先出」
图算法本质上是二叉树算法的延续
Union Find并查集算法
回溯算法
回溯法 采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
回溯算法本质就是一种暴力穷举算法,虽然效率低,但是简单
回溯算法一般不会让你求最值,而是用于罗列所有无重叠的子结果
回溯算法和dfs的区别:
DFS 是一个劲的往某一个方向搜索,而回溯算法建立在 DFS 基础之上的,但不同的是在搜索过程中,达到结束条件后,恢复状态,回溯上一层,再次搜索。因此回溯算法与 DFS 的区别就是有无状态重置
何时使用回溯算法:
当问题需要 “回头”,以此来查找出所有的解的时候,使用回溯算法。即满足结束条件或者发现不是正确路径的时候(走不通),要撤销选择,回退到上一个状态,继续尝试,直到找出所有解为止
- 找到一个可能存在的正确的答案;
- 在尝试了所有可能的分步方法后宣告该问题没有答案。
「回溯算法」强调了「深度优先遍历」思想的用途,用一个 不断变化 的变量,在尝试各种可能的过程中,搜索需要的结果。强调了 回退 操作对于搜索的合理性。
1 | //回溯算法框架伪代码 |
递归之后需要做和递归之前相同的逆向操作,实例可以参考全排列问题
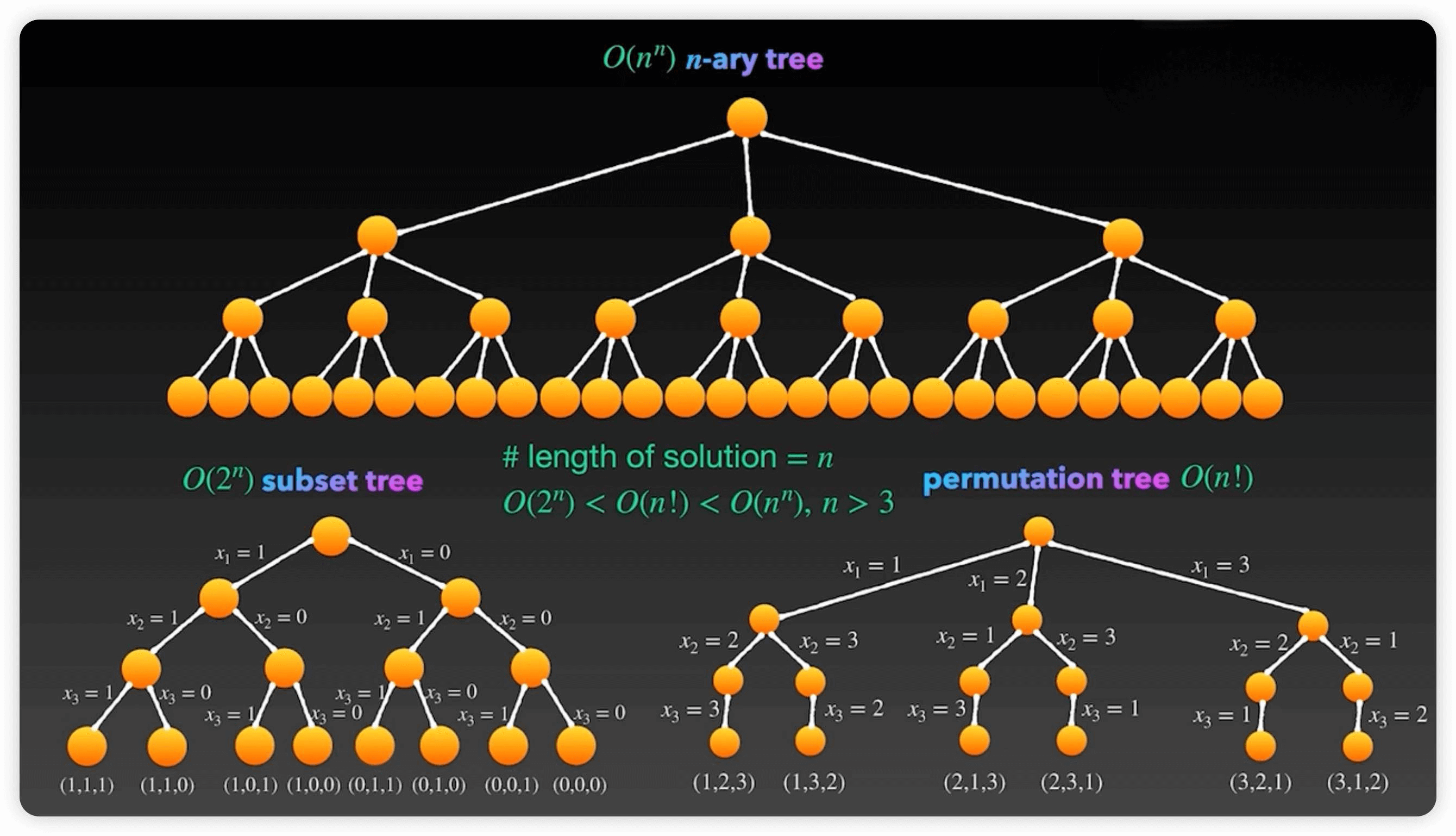
可以使用排列树和子集树来理解回溯算法 子集树参考78.子集 排列树参考46.全排列
下图中:最上方为N叉树,左下角为子集树,右下角为排列树
引力模拟算法
一些算法技巧
double类型带容差的哈希判断
1 | using System; |
先把 double 值除以容差,得到它在“第几个容差区间”
如:
obj = 1.23,_tolerance = 0.1,则1.23 / 0.1 = 12.3对结果四舍五入,得到最近的区间编号
Math.Round(12.3) = 12,表示 1.23 属于第 12 个容差区间再乘回容差,得到这个区间的“中心值”
12 * 0.1 = 1.2,所以 1.23 被归到 1.2 这个区间用这个“区间中心值”来生成哈希码。这样,只要两个 double 落在同一个容差区间,它们的 HashCode 就一样。
异或运算
- 0 ⊕ 0 = 0
- 1 ⊕ 0 = 1
- 0 ⊕ 1 = 1
- 1 ⊕ 1 = 0
- 任何数和0做异或运算,结果仍然是原来的数,即:${a\oplus0=a}$
- 任何数和其自身做异或运算,结果是0,即:${a\oplus a=0}$
- 异或运算满足交换律和结合律,即:$a\oplus b\oplus a=b\oplus a\oplus a=b\oplus(a\oplus a)=b\oplus0=b$
给你一个 非空 整数数组
nums,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
解法如下:
1 | int singleNumber(vector<int>& nums) { |
Boyer-Moore投票算法
如果一个数组有大于一半的数相同,那么任意删去两个不同的数字,新数组还是会有相同的性质(即数组有大于一半的数相同)
思路详解:
同归于尽消杀法 :
由于多数超过50%, 比如100个数,那么多数至少51个,剩下少数是49个。
- 第一个到来的士兵,直接插上自己阵营的旗帜占领这块高地,此时领主 winner 就是这个阵营的人,现存兵力 count = 1。
- 如果新来的士兵和前一个士兵是同一阵营,则集合起来占领高地,领主不变,winner 依然是当前这个士兵所属阵营,现存兵力 count++;
- 如果新来到的士兵不是同一阵营,则前方阵营派一个士兵和它同归于尽。 此时前方阵营兵力count –。(即使双方都死光,这块高地的旗帜 winner 依然不变,因为已经没有活着的士兵可以去换上自己的新旗帜)
- 当下一个士兵到来,发现前方阵营已经没有兵力,新士兵就成了领主,winner 变成这个士兵所属阵营的旗帜,现存兵力 count ++。
就这样各路军阀一直以这种以一敌一同归于尽的方式厮杀下去,直到少数阵营都死光,那么最后剩下的几个必然属于多数阵营,winner 就是多数阵营。(多数阵营 51个,少数阵营只有49个,死剩下的2个就是多数阵营的人)
最优解法如下:
1 | int majorityElement(vector<int>& nums) { |
快慢指针
链表中如何在一次遍历中找到中间节点,可以使用快慢指针
慢指针一次走一步,快指针一次走两步,快慢指针同时出发。当快指针移动到链表的末尾时,慢指针恰好到链表的中间。通过慢指针将链表分为两部分
适用于所有链表的比例定位问题
Floyd判圈算法
问题:如何检测一个链表是否有环,如果有,那么如何确定环的起点?如何确定环的长度?
「Floyd 判圈算法」(又称龟兔赛跑算法)
Floyd判圈算法(Floyd Cycle Detection Algorithm),又称龟兔赛跑算法(Tortoise and Hare Algorithm),是一个可以在有限状态机、迭代函数或者链表上判断是否存在环,求出该环的起点与长度的算法。该算法据高德纳称由美国科学家罗伯特·弗洛伊德发明。
假想「乌龟」和「兔子」在链表上移动,「兔子」跑得快,「乌龟」跑得慢。当「乌龟」和「兔子」从链表上的同一个节点开始移动时,如果该链表中没有环,那么「兔子」将一直处于「乌龟」的前方;如果该链表中有环,那么「兔子」会先于「乌龟」进入环,并且一直在环内移动。等到「乌龟」进入环时,由于「兔子」的速度快,它一定会在某个时刻与乌龟相遇,即套了「乌龟」若干圈。
原理理解:
参阅上面视频,公式推导得到以下定理:

- 有限时间内都从起点出发,快慢指针必然相遇且相遇点在环上:一定会相遇是基于有一个指针每个节点都走到了
- 在环上相遇的等速指针必定在环的入口处相遇 ==推导=> [1找到的相遇点]和起点的等速指针将在环的入口处相遇


- 判断是否有环
定义两个指针p1与p2,起始时,都指向链表的起点A,p1每次移动1个长度,p2每次移动2个长度。如果p2在移到链表的尾端时,并未与p1相遇,表明链表中不存在环。如果p1与p2相遇在环上的某一点C,表明链表有环。
- 环的长度
将指针p1固定在相遇位置C,从C点移动p2,每次移动1个长度,并用变量cnt计数。当p2再次与p1相遇时,此时cnt的值就是环的长度。
- 环的起点
环的起点即图中点B,将指针p1指向链表的起始位置A,指针p2仍在位置C,指针p1与p2每次均移动一个单位,p1与p2再次相遇的位置就是环的起点位置点B。
还有更高效率的做法:Brent的移动的兔子和传送的乌龟,参阅此链接
链表中的哑节点
哑节点的意义:
简化插入和删除操作:哑节点可以作为链表的起始节点,使得插入和删除操作在任意位置都可以统一处理。无论是在链表头部、中间还是尾部插入或删除节点,都不需要特殊处理边界情况。
处理空链表:当链表为空时,哑节点可以作为链表的唯一节点,避免了对空链表的额外判断和处理。这样,在处理链表时,不需要单独考虑链表为空的情况。
简化遍历操作:哑节点可以作为链表的起始节点,使得遍历链表时不需要对头节点进行特殊处理。遍历操作可以从哑节点的下一个节点开始,一直遍历到链表的末尾。
提高代码的一致性和可读性:通过使用哑节点,链表的操作可以统一处理,减少了重复的代码和特殊情况的处理,使得代码更加简洁、一致和易于理解。
需要注意的是,哑节点并不存储实际的数据,它的存在仅仅是为了简化链表的操作。在实际应用中,根据具体的需求和场景,可以选择在链表的头部或尾部添加哑节点。
使用哑节点的问题代码案例:
1 | ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) { |
前缀和
可以将求子数组的和为k问题转化为求解两个前缀和之差等于k的问题,通过这种方式在某些题型中可以降低一维
解法如下:
1 | /* |
差分数组
荷兰国旗问题
Dutch National Flag Problem 荷兰国旗问题,该问题由荷兰计算机科学家Dijkstra所提出
怎么对一组数做划分,左边都小于他,右边都大于他,中间都等于他(不要求有序,只要求对数组进行划分)
参考leetcode的75. 颜色分类
解决代码如下:
1 | //双指针,转移+修正 |
巧妙的递归解法思路盘点
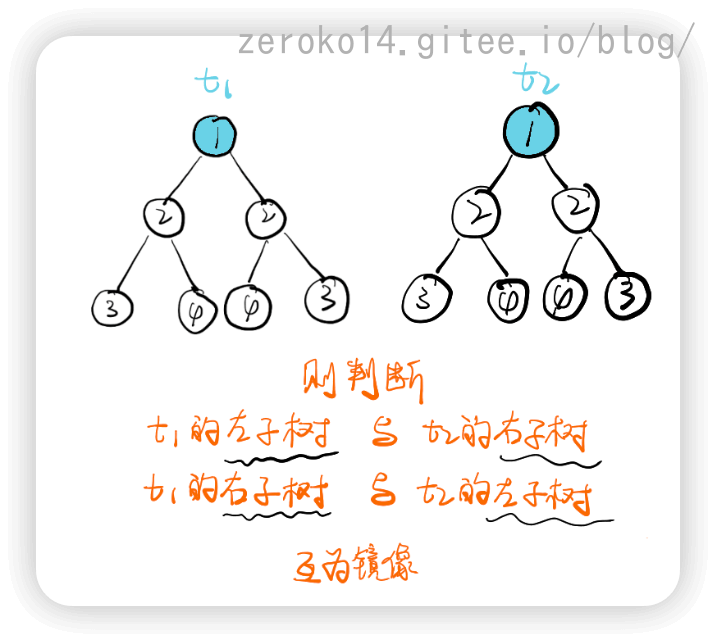
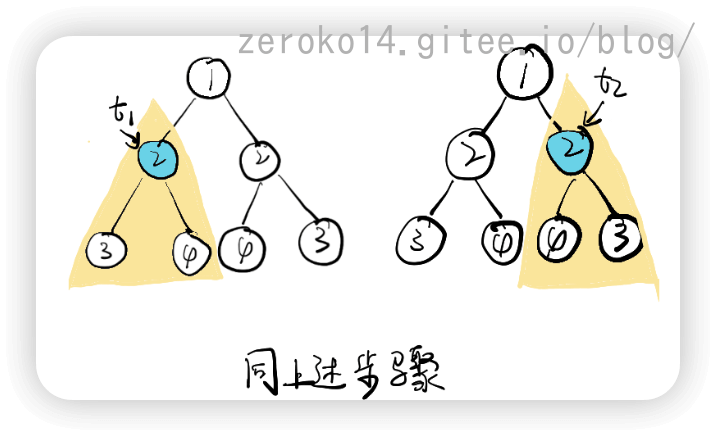
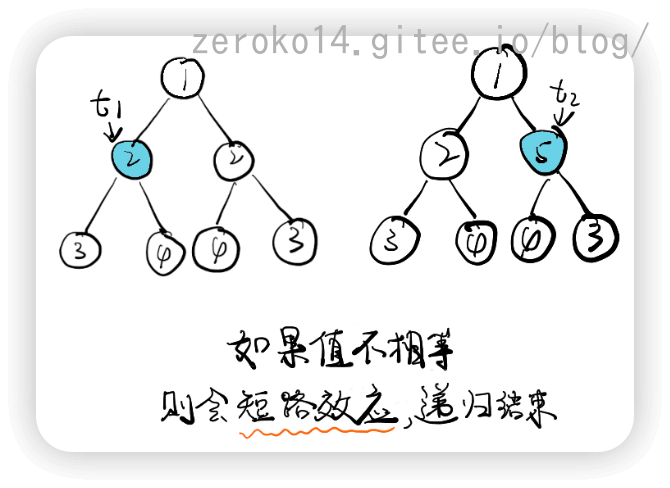
对称二叉树
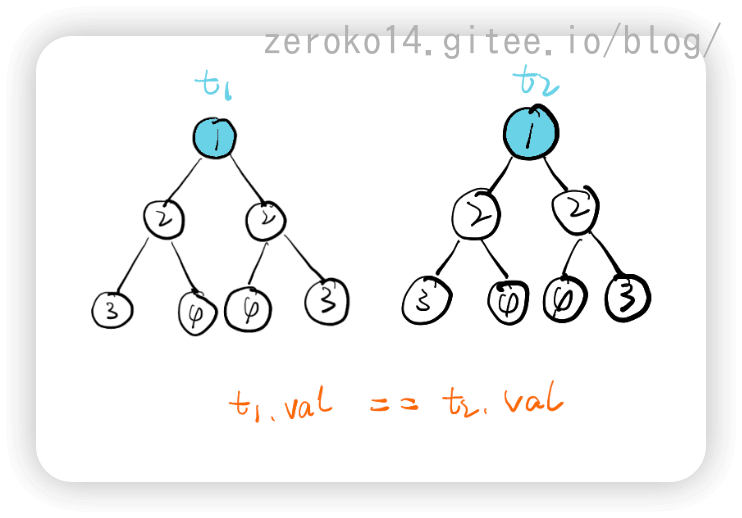
递归解法:
1 | //比较两棵树是否对称二叉树 |
该题思路的重点在于将一棵树,当成两棵树来比较
图解如下:
改成迭代方式代码如下: (比较抽象)
引入一个队列,这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值(队列中每两个连续的结点应该是相等的,而且它们的子树互为镜像),然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时,或者我们检测到树不对称(即从队列中取出两个不相等的连续结点)时,该算法结束。
1 | class Solution { |
全排列
伪代码

遍历流程

代码
1 | vector<vector<int>> permute(vector<int> &nums) |
此代码后面使用交换的方式,避免了”检测是否已经重复处理过”的时间复杂度
子集
这一题找了半天都没有找到递归规律,看了题解才明白,遂记录下来
- 开始假设输出子集为空子集
- 遍历数组,对于数组中的每一个整数,每一步都向输出子集中所有子集添加这个整数,并生成新的子集。

gif最后少了一个3的子集,是bug
解法如下:
1 | vector<vector<int>> subsets(vector<int>& nums) { |
假设 nums 中的元素个数为n,则 nums 的子集个数为$2^n$。
时间复杂度:$O(n•2^n)$
空间复杂度:$O(n•2^n)$
巧妙的算法解决记录
15.三数之和
1 | vector<vector<int>> threeSum(vector<int>& nums) { |
代码执行流程

128.最长连续序列
记录的这个代码主要是精彩在一次遍历解决问题
- 哈希map的key为: 数组中的数,
- value为: 遍历到该元素时,如果 key 是某个连续区间的左/右端点,则 value 为该连续区间的长度;否则 value 值无意义
伪代码:
若数已在哈希表中:跳过不做处理
若是新数加入:
取出其左右相邻数已有的连续区间长度 left 和 right
计算当前数的区间长度为:cur_length = left + right + 1
根据 cur_length 更新最大长度 max_length 的值
更新区间两端点的长度值
本质上就是利用map的value来储存正在处理的数以及他左右的数的序列长度,也即是通过value来动态叠加连续序列长度
1 | int longestConsecutive(vector<int>& nums) { |
878.第N个神奇数字
解题思路: 二分查找+容斥原理
a,b找神奇数字,1到x范围内的神奇数字的个数为:x/a+x/b-x/ab,于是就可以使用二分查找不断逼近第n个神奇数字的位置
而x必然是min(a,b)*n
待解决
230题使用中序morris遍历算法报栈溢出错误?待解决