计算机组成原理

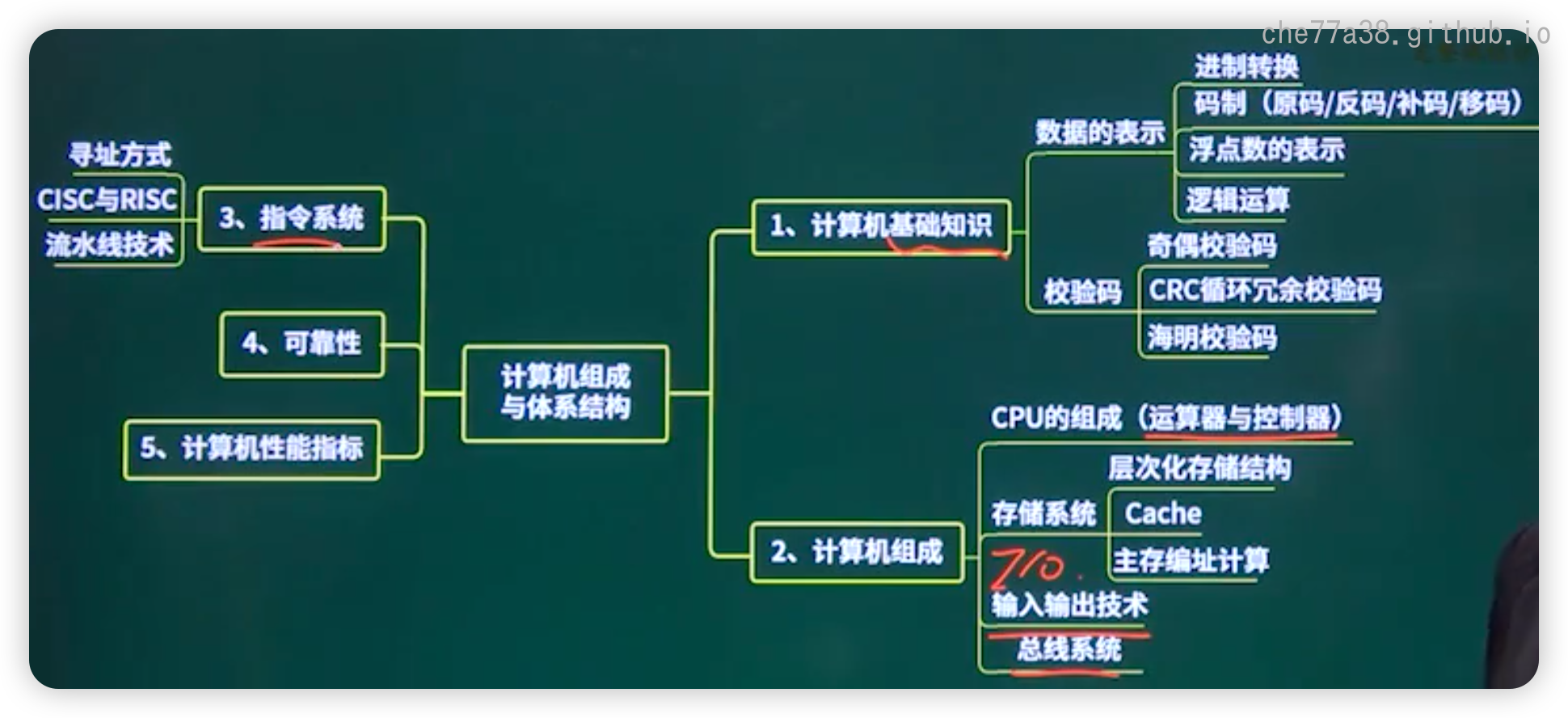
计算机组成原理是研究计算机系统内部结构、工作原理及其相互关系的一门学科

参考视频

image-20250318095929421

image-20250318100017168

数值相关

进制转换

小数部分转二进制

十进制0.625转二进制为0.101,转化方法如下:

image-20241216095040516 $$ 0.625 = 1\times0.5 + 0\times0.25+1\times0.125=1\times2^{-1}+0\times2^{-2}+1\times2^{-3} $$

大于1的部分转二进制

除基取余法,注意余数要倒着排列

image-20250228174201926

得到的结果为1011110

十六进制与二进制转换

image-20241216095753476

所以只需要按照4位二进制进行分割,将每个4位二进制计算出来就是16进制的一位

码制

  • 原码 最高位是符号位,其余低位表示数值的绝对值
  • 反码 正数的反码与原码相同,负数的反码是其绝对值按位取反(符号位不变)
  • 补码 正数的补码与原码相同,负数的补码是其反码末位加1(符号位不变)
  • 移码 补码的符号位按位取反

存在意义

  • 原码：直观简单，适合人类阅读和简单应用。
  • 反码：简化减法，是补码的过渡形式。
  • 补码：运算高效、零唯一，广泛用于现代计算机。
  • 移码：便于比较，常用于浮点数指数。
类型 数值1 数值-1 1 加 -1
原码 0000 0001 1000 0001 1000 0010
反码 0000 0001 1111 1110 1111 1111
补码 0000 0001 1111 1111 0000 0000
移码 1000 0001 0111 1111 1000 0000

可见,原码/反码/移码的加法计算结果都是不对的,只有补码的计算结果是正确的

码制 定点数 定点小数 数码个数
原码 $-(2^{n-1}-1) ~+ (2^{n-1}-1)$ $-(1-2^{n-1}) ~+ (1-2^{n-1})$ $2^n-1$
反码 $-(2^{n-1}-1) ~+ (2^{n-1}-1)$ $-(1-2^{n-1}) ~+ (1-2^{n-1})$ $2^n-1$
补码 $-2^{n-1}-1 ~+ (2^{n-1}-1)$ $-1 ~+ (1-2^{n-1})$ $2^n$
移码 $-2^{n-1}-1 ~+ (2^{n-1}-1)$ $-1 ~+ (1-2^{n-1})$ $2^n$

p.s. 补码中的10000000是-128,而不再是-0

补码计算对应值的方式

  • 如果最高位是0(正数),直接二进制转十进制
  • 如果最高位是1(负数),需要进一步处理
    • 取反: 所有位按位取反
    • 加1: 取反结果上加1,得到正数的二进制形式
    • 转十进制: 将结果转为十进制
    • 加负号: 在结果前加负号

定点数（Fixed-point number）是一种数值表示方法，其中小数点的位置是固定的，不会随着数值的改变而移动。小数点的位置通常由设计者在数据位中提前指定，可以位于任意位置，例如数据位的中间、最左边或最右边。定点数的表示范围和精度取决于小数点的位置以及数据位的长度
定点小数（Fixed-point fractional number）是定点数的一种特殊形式，其中小数点的位置固定在数据位的特定边界，通常是最右边（在某些情况下也可能是最左边，但常见的是最右边）。这意味着所有数据位都用于表示小数部分，没有整数部分

格式:

定点小数格式

定点小数通常用于表示纯小数值

浮点数

实际运算在软考测试中并未出现过
$$
浮点数 = 尾数 \times 2^{阶码}
$$
这里指数也可以叫阶码,基数固定为2

  • 指数/阶码 使用 移码表示
  • 尾数 使用 补码表示(IEEE754的格式尾数是用原码表示)

运算过程: 对阶(阶码小的向阶码大的对齐,即阶码小的尾数右移实现) -> 尾数计算 -> 结果格式化(使结果介于0.5到1之间)

浮点数的运算过程案例参考此处

16位浮点数,阶符1位,阶码6位,数符1位,尾数8位,若阶码用移码表示,尾数用补码表示,则该浮点数所能表示的数值范围是$-2^{63}$ ~ $(1-2^{-8}) \times 2^{63}$

  • 阶码的位数决定表示范围,位数越多,范围越大
  • 尾数的位数决定数的有效精度,位数越多,精度越大

逻辑运算

运算符优先次序

!(非)> 算数运算符(先乘除后加减) > 关系运算符(先大小比较,再等于判断,最后不等于判断) > &&(与) > ||(或) >赋值运算符

短路原则

在逻辑表达式的求解中,并不是所有的逻辑运算符都要被执行

  1. a&&b&&c只有a为真时,才需要判断b的值,只有a和b都为真时,才需要判断c的值
  2. a||b||c只要a为真,就不必判断b和c的值,只有a和b都为假,才判断c

逻辑门

【笔记】逻辑门图解—与门、或门、非门、与非门、或非门、异或门、同或门_八种逻辑门电路原理图

与或非三种逻辑门可以构建整个逻辑大厦

符号是抽象的,无关实现的,具体实现可以是继电器,电子管,晶体管,甚至水管等.早期计算机中使用的是电子管及部分继电器实现,而现代计算机使用的是晶体管

校验码

基础知识盘点:

  • 码距: 任何一种编码都由许多码字构成,任意两个码字之间最少变化的二进制位数就称为数据校验码的码距
校验码位数 校验码位数 校验码位置 检错 纠错 校验方式
奇偶校验 1 一般拼接在头部 可检奇数位错 不可纠错 奇校验：最终1的个数是奇数个；
偶校验：最终1的个数是偶数个；
CRC循环冗余校验 生成多项式式最高次幂决定 拼接在信息位尾部 可检错 不可纠错 模二除法求余数，拼接作校验位
海明校验 $2^r ≥ m + r + 1$ 插入在信息位中间 可检错 可纠错 分组奇偶校验

现在海明码比起现代Reed-Solomon算法,应用没那么广泛了,这也是CD和DVD中现在实际使用的纠错算法
Turbo 码是一种高效的纠错码，通常用于无线通信系统。它由两个或多个简单的卷积码和一个交织器组成

奇偶校验码

奇偶校验码的编码方法是：由若干位有效信息（如一个字节），再加上一个二进制位（校验位）组成校验码。

  • 奇校验：整个校验码（有效信息位和校验位）中“1”的个数为奇数。
  • 偶校验：整个校验码（有效信息位和校验位）中“1”的个数为偶数。

收到信息,首先检查”1”的个数,是否符合标准,若不符合标准,则表示校验失败

通信过程中,大部分情况只有一个比特位的错误

奇偶校验,可检查奇数个数据位的错误,不可纠错 (因为偶数个数据位出错会刚好抵消奇偶性变化)

CRC循环冗余校验码

CRC的编码方法是：在k位信息码之后拼接r位校验码。

应用CRC码的关键是如何从k位信息位简便地得到r位校验位(编码),以及如何从k+r位信息码判断是否出错。

把接收到的CRC码用约定的生成多项式G(X)去除（模二除法也就是异或操作），如果正确，则余数为0；如果某一位出错，则余数不为0。不同的位数出错其余数不同，余数和出错位序号之间有唯一的对应关系。

手算参考视频

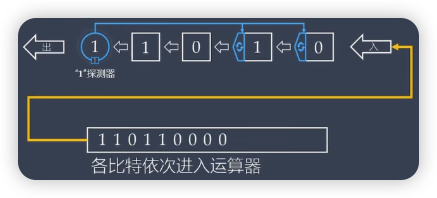
先在数据串末尾加0(0的数量为{CRC除数的长度减1})->将数据串的第一个1与CRC除数左对齐，每一位按位异或->将未处理的数据搬下来作为新数据串与CRC除数进行上一步中的运算->最终得到的校验和的长度为{CRC除数的长度减1}

手算

[[算法#CRC校验算法|代码参考]]

image-20250306090528277

上图中模拟的是CRC除数为10011的情况

海明校验码

3Blue1Brown可视化参考视频

海明码既可检错,也可纠错

其巧妙之处在于: 只少用了一点空间,就可以定位并修改任意的单个错误,如果利用上0位作为整体的奇偶校验(拓展海明校验码),还能发现2个错误,虽然只能修正其中一个

iShot_2025-03-06_10.01.28

海明校验码的原理是：在有效信息位中加入几个校验位形成海明码，使码距比较均匀地拉大，并把海明码的每个二进制位分配到几个奇偶校验组中。当某一位出错后，就会引起有关的几个校验位的值发生变化，这不但可以发现错误，还能指出错误的位置，为自动纠错提供了依据

海明校验码位数的求取符合如下公式
$$
2^{校验码位数} \geq 信息码位数+校验码位数+1
$$
如16位信息码,至少需要海明校验码5位

以5位海明校验码为例,他们所放的位置分别是$2^0,2^1,2^2,2^3,2^4$位置

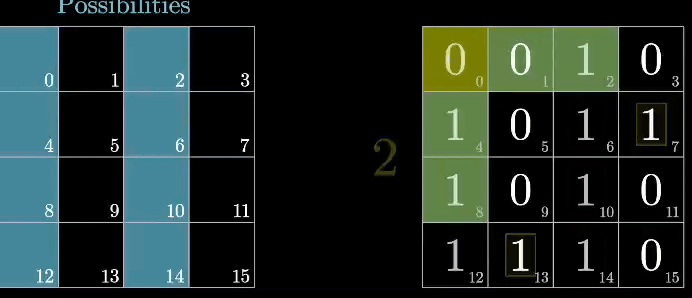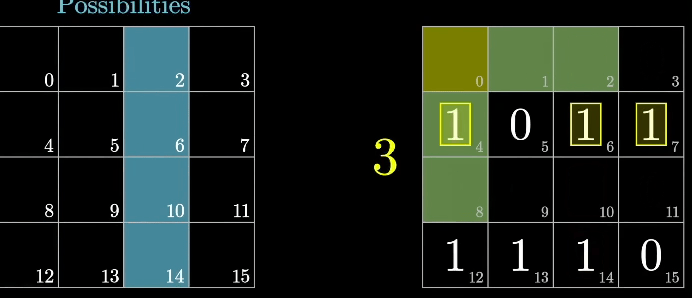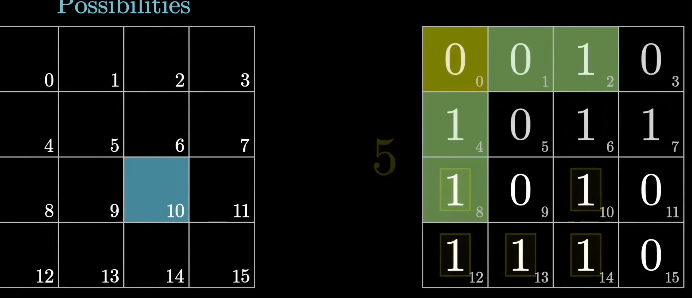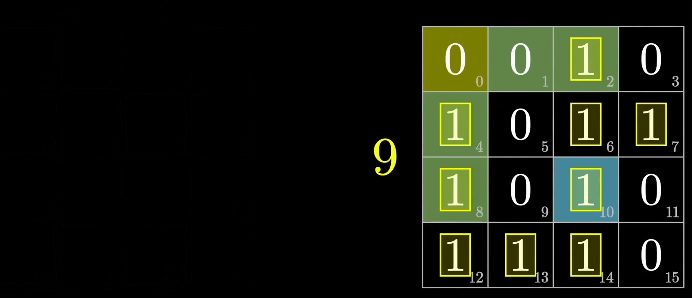
某海明码表示D9,D8,D7,D6,D5,D4,P4,D3,D2,D1,P3,D0,P2,P1

数据位D9由P4,P3,和P2进行校验 从右到左D9的位序为14(0b1110) = 8+4+2,所以是P4,P3和P2

数据位D5由P4和P2进行校验 从右到左的位序为10(0b1010) = 8+2,所以是P4和P2

计算机结构

  • 主机
    • 主存储器/内存
    • CPU(中央处理单元)
      • 运算器
      • 控制器
  • 外设
    • 输入设备,如鼠标键盘
    • 输出设备,如显示器
    • 辅助存储器/外存,如u盘,光盘,硬盘等(虽然处在主机内部,但是属于外设)
image-20250310085751315

CPU的组成

CPU是由在控制器的控制下,运算器,存储器和输入输出设备等部件构成了一个整体

CPU

  • 控制器
  • 运算器
image-20250310091202990

控制器

控制整个CPU的工作,控制器是整个系统的指挥中心

控制器

  • 程序计数器PC: 存放下一条指令在内存中的地址
  • 指令寄存器IR: 存放即将要执行的指令
  • 指令译码器ID: 翻译指令(操作码+操作地址)
  • 地址寄存器AR: 保存当前CPU所访问的内存地址
  • 时序部件: 提供时序控制信号(计算机时钟)

口诀: 寄存遗址时

运算器

执行算术运算(加减乘除等)和逻辑运算(与或非等)

  • 算术逻辑单元ALU: 实现对数据的算数和逻辑运算
  • 累加寄存器AC: 通用寄存器,为ALU提供一个工作区,暂存源操作数和结果
  • 数据缓冲寄存器DR: cpu与存储交换的过渡区.读写内存,暂存的指令或数据
  • 状态条件寄存器PSW: 存状态标志及控制标志

口诀:

  1. 鸡 (逻辑)
  2. 同 (通用寄存器)
  3. 树 (数据缓冲)
  4. 撞 (状态寄存器)

指令的执行流程

取址:

PC(程序计数器)->AR(地址寄存器)->DR(数据缓冲寄存器)->IR(指令寄存器)

分析:

OP(IR) -> CU(控制单元)

执行:

Ad(IR) -> AR(地址寄存器) -> DR(数据缓冲寄存器) -> AC(累加器)

iShot_2025-02-02_19.43.03 CPU组成

寻址方式

一条指令就是机器机器语言的一个语句,它是一组有意义的二进制代码,指令基本格式如下:

image-20250310091644576

实际的情况可以参考[[PE]]

寻址方式如下:

  • 立即寻址方式: 操作数直接在指令中,速度快,灵活性差
  • 直接寻址方式: 指令中存放的是操作数的地址
  • 间接寻址方式: 指令中存放了一个地址,这个地址对应的内容是操作数的地址
  • 寄存器寻址方式: 寄存器存放操作数
  • 寄存器间接寻址方式: 寄存器中存放的是操作数的地址
image-20250310093046176

指令集

  • CISC：复杂，指令数量多，频率差别大，多寻址
  • RISC：精简，指令数量少，操作寄存器，单周期，少寻址，多通用寄存器，流水线
指令系统类型 指令 寻址方式 实现方式 其它 实际指令集
CISC (复杂) 数量多，使用频率差别大，可变长格式 支持多种寻址方式 微程序控制(微码) 研制周期长 intel x86
RISC (精简) 数量少，使用频率接近，定长格式，大部分为单周期指令，操作寄存器，只有 Load/Store 才操作内存 支持的寻址方式少 增加了通用寄存器；硬布线逻辑控制为主，适合采用流水线 优化编译,有效支持高级语言 ARM,RISC-V

流水线技术

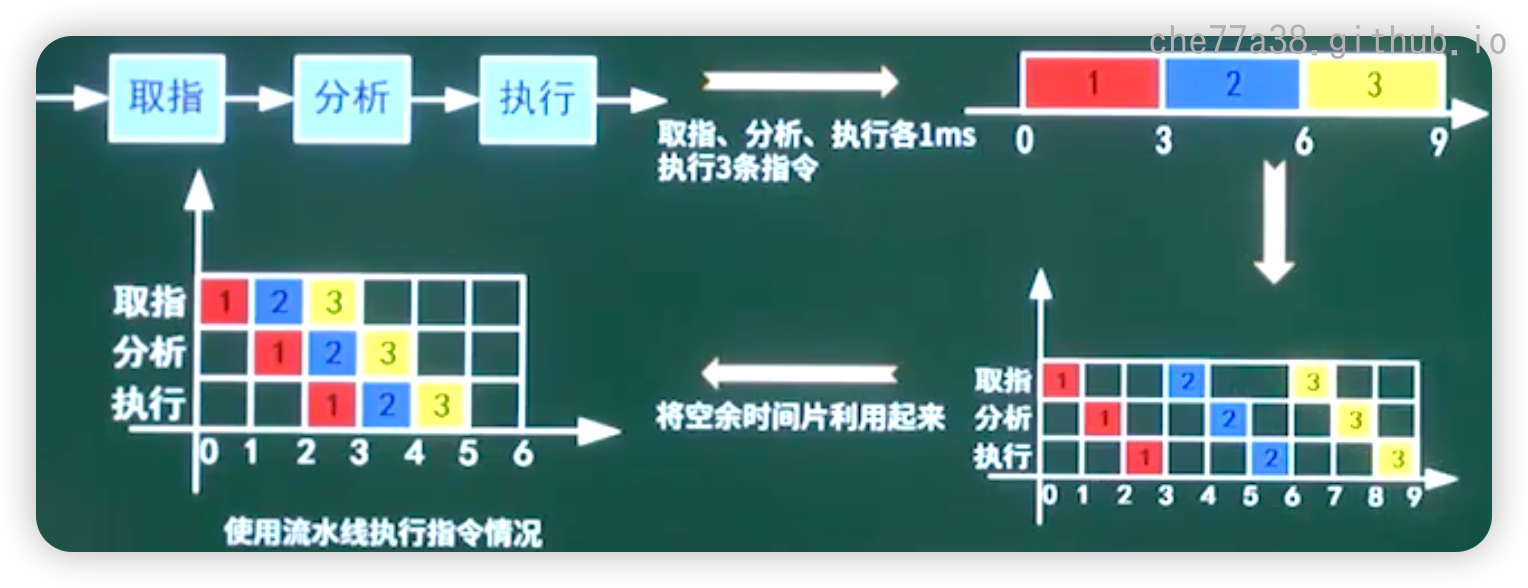
流水线是指在程序执行时多条指令重叠进行操作的一种准并行处理实现技术。
各种部件同时处理是针对不同指令而言的，它们可同时为多条指令的不同部分进行工作，以提高各部件的利用率和指令的平均执行速度

image-20250311085424341

相关参数计算：流水线执行时间计算、流水线吞吐率、流水线加速比、流水线效率

流水线执行时间计算

image-20250311090213403

流水线周期为执行时间(如,取址,分析,执行中)最长的一段
$$
流水线计算公式 = 1条指令执行时间+(指令条数-1) \times 流水线周期
$$

$$
理论公式:(t_{1}+t_{2}+…+t_{k})+(n-1) * t
$$

$$
实践公式:k*t+(n-1)*t
$$

image-20250311092238347

实践公式和理论公式的区别是流水线建立时间,第一条指令的执行时间做了一些冗余,划分为三个段,每个段都以流水线周期为准

例题如下:

一条指令的执行过程可以分解为取指,分析和执行三步,

  • 取址时间$t_{取指}=3Δt$
  • 分析时间$t_{分析}=2Δt$
  • 执行时间$t_{执行}=4Δt$

若按串行方式执行,则10条指令全部执行完需要(90)Δt

若按流水线方式执行,则流水线周期为(4)Δt,10条指令全部执行完需要(45)Δt

计算理论公式为(3+2+4)+(10-1)*4

计算实践公式为:(4+4+4)+(10-1)*4

考试的过程中默认使用理论公式来计算

流水线吞吐率计算

流水线的吞吐率（Though Put rate,TP）是指在单位时间内流水线所完成的任务数量或输出的结果数量。计算流水线吞吐率的最基本的公式如下：

流水线吞吐率计算公式
$$
TP = \frac {指令条数} {流水线执行时间(理论公式)}
$$
流水线最大吞吐率计算公式
$$
TP_{\max}=\lim_{n\to\infty}\frac{n}{流水线执行时间(实践公式)}=\lim_{n\to\infty}\frac{n}{(k+n-1)t}=\frac{1}{t}
$$
上述公式中:n是指令条数,k是分段数,t是流水线周期

例题如下:

一条指令的执行过程可以分解为取指、分析和执行三步

  • 取址时间$t_{取指}=3Δt$
  • 分析时间$t_{分析}=2Δt$
  • 执行时间$t_{执行}=4Δt$

10条指令的吞吐率和最大吞吐率是多少?

吞吐率 = 10 / 45Δt

最大吞吐率 = 1 / 4Δt

流水线加速比/流水线效率

这两项在软考高级中才考

存储系统

必考

层次化存储体系

image-20250311111655478

局部性原理是层次化存储结构的支撑

  • 时间局部性: 刚被访问的内容,立刻又被访问
  • 空间局部性: 刚被访问的内容,临近的空间很快被访问

层次化存储结构分类

存储器位置: 内存 & 外存

存取方式

  1. 按内容存取: 相联存储器(如Cache)

  2. 按地址存取:

    • 随机存取存储器(如内存)

    • 顺序存取存储器(如磁带)

    • 直接存取存储器(如磁盘) 结合上面两种方式

      移臂调度过程是随机存取,旋转延迟的过程是顺序存取

工作方式

  • 随机存取存储器RAM(如内存DRAM) 掉电会丢失
  • 只读存储器ROM(如BIOS)
  • DRAM: 动态随机存取存储器
  • SRAM: 静态随机存取存储器 比DRAM成本高一些
  • Cache: 高速缓存
  • FEPROM: 电可擦可编程只读存储器

Cache

在计算机的存储系统体系中，Cache是访问速度最快的层次（若有寄存器，则寄存器最快）

Cache改善系统性能的依据是程序的局部性原理

Cache就是从主存复制了一部分内容到Cache中,cpu在取数据的时候,如果Cache内已经存在,则不需要访问主存了

命中率

“Cache+主存储器”的系统的平均周期公式如下:
$$
平均周期时间 =Cache访问命中率 \times Cache周期时间+(1-Cache访问命中率) \times 主存储器周期时间
$$
其中,(1-Cache访问命中率)又称为失效率(未命中率)

Cache的命中率随容量太高会提高,但不是线性提高,而是随着容量增大,命中率的提高越来越缓慢

映像方式

主存与Cache之间的对应关系叫地址映射,也称为地址映像

分类如下:

注：主存与Cache之间的地址映射由硬件直接完成。

冲突率（高、中、低） 电路复杂度（复杂、简单、折中）
直接相匹配频率 高 简单
全相匹配频率 低 复杂
组相匹配频率 中 折中
映像过程

地址映像是将主存与Cache的存储空间划分为若干大小相同的页（或称为块）。
例如，某机的主存容量为1GB，划分为2048页，每页512KB；
Cache容量为8MB，划分为16页，每页512KB。

直接相联映像
image-20250312100531487

电路简单,但冲突率非常高

全相联映像
image-20250312100848903

冲突率低,但是电路复杂度高

组相联映像

是直接相联映射和全相联映射的折中方案

电路复杂度二者折中,冲突率二者折中

image-20250312101118023

主存编址计算

$$
存储单元个数 = 最大地址 - 最小地址 + 1
$$

编址内容

  • 按字编址: 存储体的存储单元是字存储单元,即最小寻址单位是一个字(一个存储单元是 “字长” 个位)
  • 按字节编址: 存储体的存储单元是字节存储单元,即最小寻址单位是一个字节(一个存储单元是8个位)

$$
总容量 = 存储单元个数 \times 编址内容
$$

根据存储器所要求的容量和选定的存储芯片的容量,就可以计算出所需芯片的总数,即:
$$
总片数 = 总容量 \div 每片的容量
$$

例题:

内存按字节编址，地址从A0000H到CFFFFH的内存，共有（192KB）字节，若用存储容量为64K*8bit的存储器芯片构成该内存空间，至少需要（3）片。

计算过程

  1. 第一个空

    存储单元个数为: A0000H - CFFFFH + 1 = 30000H
    总容量为: 30000H * 1B

    $3 \times (2^4)^4 \div 2^{10} = 192KB$

  2. 第二个空

    192 / 64 = 3, 需要3片

输入输出技术

早期计算机的I/O种类比较少,与主存交换信息都是通过CPU,而现代计算机的I/O种类较多,如果使用这种方式会使CPU的效率大大降低,如果想要提高资源利用率,那么我们就必须引入了一些机制,来让整个机器工作效率变高

I/O设备与主机交换信息的几种控制方式(越往下效率越高)

程序查询式

程序控制（查询）方式：分为两种

  • 无条件传送
  • 程序查询方式

方法简单，硬件开销小，但I/O能力不高，严重影响CPU的利用率

由CPU通过程序不断查询I/O设备是否已做好准备,从而控制I/O设备与主机交换信息;CPU要一个字一个字的从I/O设备取出,经CPU送至主存,CPU工作效率低

image-20250227171747401

中断查询式

在启动I/O设备后，CPU不查询I/O设备是否已准备就绪，而是继续执行自身程序，只有当I/O设备准备就绪井向CPU发出中断请求后才予以响应；

中断方式因为CPU无需等待而提高了传输请求的响应速度

image-20250227171901019

中断处理过程

  • CPU无需等待也不必查询I/O状态
  • 当I/O系统准备好以后，发出中断请求信号通知CPU
  • CPU接到中断请求后，保存正在执行程序的现场（保存现场）,打断的程序当前位置即为断点
  • (通过中断向量表)转入I/O中的服务程序的执行，完成I/O系统的数据交换
  • 返回被打断的程序继续执行（恢复现场）
image-20250314091511919

DMA方式

在DMA方式中，主存与I/O设备之间有一条数据通路，DMA通过通路把数据传送到主存储器，无需CPU的参与。

DMA方式 DMA方式是为了在主存与外设之间实现高速、批量数据交换而设置的。DMA方式比程序控制方式与中断方式都高效。

（DMAC向总线裁决逻辑提出总线请求；CPU执行完当前总线周期即可释放总线控制权。此时DMA响应，通过DMAC通知I/O接口开始DMA传输。）

CPU是在(一个总线周期)结束时响应DMA请求

直接内存访问方式

image-20250227172753646 image-20250227172226354

I/O通道式

通道是用来负责管理I/O设备以及实现主存与I/O设备之间交换信息的部件，可以视为一种具有特殊功能的处理器

简单了解即可

image-20250227173627295

总线系统

总线的特点是分时双工

一条总线同一时刻仅允许一个设备发送,但允许多个设备接收

总线分类:

  • 数据总线（Data Bus）：在CPU与RAM之间来回传送需要处理或是需要储存的数据。
  • 地址总线 （Address Bus）：用来指定在RAM （Random Access Memory）之中储存的数据的地址。
  • 控制总线 （Control Bus）：将微处理器控制单元 （Control Unit）的信号，传送到周边设备。

各种总线特点

  • 并行总线适合近距离高速数据传输
  • 串行总线适合长距离数据传输
  • 专用总线在设计上可以与连接设备实现最佳匹配

系统可靠性

可靠性指标

平均无故障时间: MTTF = 1/失效率

平均故障修复时间: MTTR = 1/修复率

平均故障间隔时间: MTBF = MTTR + MTTF

系统可用性: MTTF/(MTTR+MTTF)
$$
系统可用性 = \frac {平均故障修复时间}{平均故障修复时间+平均无故障时间} = \frac {MTTF}{MTTR+MTTF}
$$
image-20250314100549002

在实际应用中,一般MTTR很小,令MTTR为1得到如下公式(非常常考)

因此,
$$
可靠性 = \frac {MTTF}{1+MTTF}
$$

串联系统与并联系统

可以利用冗余结构来提高可靠性

串联系统

串联系统只要有一个部件不可靠,就是不可靠

最短寿命的组件决定了整体寿命

image-20250314101858692

并联系统

并联系统只要有一个部件可靠就是可靠

假设每个组件独立失效，并且其寿命服从指数分布，其失效率 λ 是常数，那么系统的总失效率是各个组件失效率之和，系统寿命是它的倒数。

这意味着，如果多个组件并联，系统的寿命实际上比单个组件的平均寿命更长！换句话说，增加并联组件的数量，可以大大提升系统的可靠性和平均寿命。

image-20250314103533705

系统的可靠度 R 等于1 减去所有组件都失效的概率：
$$
R = 1 - (1 - R_1) \times (1 - R_2) \times … \times (1 - R_n)
$$
μ（系统的平均寿命），代表整个并联系统的平均寿命/平均无故障时间（MTTF）

N模混合系统可靠性计算

image-20250314110749697

性能指标

  • 字长和数据通路宽度(一次性数据线路能通过的数据量(数据脉冲))

  • 主存容量和存取速度(对于主存访问的时候,从读数据到读完回来这个操作的时间就是存取速度)

  • 运算速度

    • 主频与CPU时间周期

      主频为2.4GHz表示1s中有2.4G次脉冲

      CPU时间周期为1次脉冲的时间(单位是秒)

    • CPI与IPC

      • CPI: 平均每条指令的平均时钟周期个数(CPI,clock per instruction)
      • IPC: 每(时钟)周期运行指令条数(IPC,instruction per clock)

    • MIPS与MFLOPS

      • MIPS: 百万条指令每秒(MIPS,Million Instructions Per Second)
        $$
        \mathrm{MIPS}=\text{指令条数}/(\text{执行时间}\times10^6)=\text{主频/CPI}=\text{主频}\times\mathrm{IPC}
        $$

      • MFLOPS: 每秒百万个浮点操作(MFLOPS,Million Floating-point Operations per Second)
        $$
        \mathrm{MFLOPS}=\text{浮点操作次数}/(\text{执行时间}\times10^6)
        $$

  • 吞吐量与吞吐率

    • 吞吐量: 某一个时间间隔内完成的任务量
    • 吞吐率: 单位时间间隔内完成的任务量

  • 响应时间(RT)与完成时间(TAT)

    • 响应时间(Response Time): 提交请求之后到完成请求的时间
    • 完成时间: 事务/指令 执行完成的时间

  • 兼容性

  • 负载

    一台电脑能同时处理的请求数

例题:

某计算机系统的CPU主频为2.8GHz。某应用程序包括3类指令，各类指令的CPI（执行每条指令所需要的时钟周期数）及指令比例如下表所示。执行该应用程序时的平均CPI为(3.5);运算速度用MIPS表示，约为(800)

指令A 指令B 指令C
比例 35% 45% 20%
CPI 4 2 6

  1. 第一空:

    要使用加权平均: (35% * 4) + (45% * 2) + (20% * 6) = 3.5

    即: 平均执行一条指令需要3.5个时钟周期

  2. 第二空:

    由于CPU主频是2.8GHz,即一个时钟周期的时间为:1/2.8GHz

    一秒可以执行$\frac {1}{3.5 \times \frac {1}{2.8GHz}} = 800000000$条指令

    即为800MIPS

    p.s. $1G = 10^3M = 10^6K = 10^9$

编译过程

image-20250227175247521